Galaxy rotation curves via conformal factors
- PMID: 29681764
- PMCID: PMC5906514
- DOI: 10.1140/epjc/s10052-018-5792-2
Galaxy rotation curves via conformal factors
Abstract
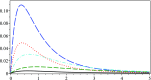
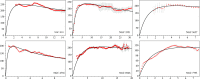
We propose a new formula to explain circular velocity profiles of spiral galaxies obtained from the Starobinsky model in the Palatini formalism. It is based on the assumption that the gravity can be described by two conformally related metrics: one of them is responsible for the measurement of distances, while the other, the so-called dark metric, is responsible for a geodesic equation and therefore can be used for the description of the velocity profile. The formula is tested against a subset of galaxies taken from the HI Nearby Galaxy Survey (THINGS).
Figures
Similar articles
-
Six spiral galaxies lacking dark matter.Sci Rep. 2024 Jul 27;14(1):17268. doi: 10.1038/s41598-024-68144-w. Sci Rep. 2024. PMID: 39068188 Free PMC article.
-
Strongly baryon-dominated disk galaxies at the peak of galaxy formation ten billion years ago.Nature. 2017 Mar 15;543(7645):397-401. doi: 10.1038/nature21685. Nature. 2017. PMID: 28300118
-
Self-Interacting Dark Matter Can Explain Diverse Galactic Rotation Curves.Phys Rev Lett. 2017 Sep 15;119(11):111102. doi: 10.1103/PhysRevLett.119.111102. Epub 2017 Sep 13. Phys Rev Lett. 2017. PMID: 28949220
-
Balance of dark and luminous mass in rotating galaxies.Phys Rev Lett. 2005 Oct 21;95(17):171302. doi: 10.1103/PhysRevLett.95.171302. Epub 2005 Oct 20. Phys Rev Lett. 2005. PMID: 16383816
-
Impact of a global quadratic potential on galactic rotation curves.Phys Rev Lett. 2011 Mar 25;106(12):121101. doi: 10.1103/PhysRevLett.106.121101. Epub 2011 Mar 23. Phys Rev Lett. 2011. PMID: 21517292
References
-
- A. Einstein, Sitzungsber. Preuss. Akad. Wiss. Berlin (Math. Phys.) 1915(part 2), 844–847 (1915)
-
- Einstein A. Ann. Phys. 1916;49:769–822. doi: 10.1002/andp.19163540702. - DOI
-
- Einstein A. Ann. Phys. 2005;14:517. doi: 10.1002/andp.200590044. - DOI
-
- Huterer D, Turner MS. Phys. Rev. D. 1999;60:081301. doi: 10.1103/PhysRevD.60.081301. - DOI
-
- Sami EJ, Tsujikawa MS. Int. J. Mod. Phys. D. 2006;15:1753–1935. doi: 10.1142/S021827180600942X. - DOI
LinkOut - more resources
Full Text Sources
Other Literature Sources
