Numerical Simulations of the Motion and Deformation of Three RBCs during Poiseuille Flow through a Constricted Vessel Using IB-LBM

Abstract

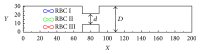
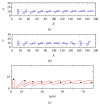
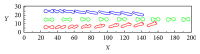
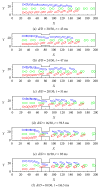
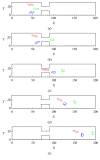
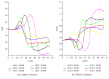
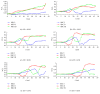
The immersed boundary-lattice Boltzmann method (IB-LBM) was used to examine the motion and deformation of three elastic red blood cells (RBCs) during Poiseuille flow through constricted microchannels. The objective was to determine the effects of the degree of constriction and the Reynolds (Re) number of the flow on the physical characteristics of the RBCs. It was found that, with decreasing constriction ratio, the RBCs experienced greater forced deformation as they squeezed through the constriction area compared to at other parts of the microchannel. It was also observed that a longer time was required for the RBCs to squeeze through a narrower constriction. The RBCs subsequently regained a stable shape and gradually migrated toward the centerline of the flow beyond the constriction area. However, a sick RBC was observed to be incapable of passing through a constricted vessel with a constriction ratio ≤1/3 for Re numbers below 0.40.

Figure 1

Schematic descriptions of the physical RBC models.

Figure 2

D2Q9 lattice.

Figure 3

Structural boundary immersed in the 2D computational domain.

Figure 4

Physical model of the cross-sectional profile of an RBC of length L, width W, and radius R.

Figure 5

The rotational motions of an initially spherical vesicle in Poiseuille flows: (a) series of snapshots from experimental data [34], (b) numerical simulation by the FE-LBM [35], and (c) current numerical simulation.

Figure 6

The time evolutions of the motions of RBC in Poiseuille flows, the initially vertical RBCs are positioned near the bottom lateral wall of the channel. (a) Healthy RBC, (b) sick RBC, and (c) numerical simulation by the FE-LBM [35].

Figure 7

Rotational motions of healthy RBC ((a) and (c)) and sick RBC ((b) and (d)) in Poiseuille flows. The initially thwart-wise RBCs are positioned near the bottom lateral wall of the channel. ((a) and (b)) Current numerical simulation and ((c) and (d)) numerical results of [9].

Figure 8

Rotational motions of three healthy RBCs asymmetrically positioned in the channel.

Figure 9

Variation of the RBC vertical movements with respect to the Re number of the flow: (a) the relationship of t and vertical distance and (b) the effect of Re on the barycentric coordinates.

Figure 10

Transient deformations and motions of three healthy RBCs during Poiseuille flow through a constricted vessel: (a) d/D = 30/30 at t = 45 ms, (b) d/D = 24/30 at t = 47 ms, (c) d/D = 20/30 at t = 51 ms, (d) d/D = 16/30 at t = 59.5 ms, (e) d/D = 12/30 at t = 85 ms, and (f) d/D = 12/30 at t = 116.5 ms.

Figure 11

Transient deformations and motions of three sick RBCs during Poiseuille flow through a contracted vessel with Re = 0.10: (a) d/D = 30/30 at t = 46.5 ms, (b) d/D = 24/30 at t = 47.5 ms, (c) d/D = 20/30 at t = 51.5 ms, (d) d/D = 16/30 at t = 62 ms, (e) d/D = 12/30 at t = 88 ms, and (f) d/D = 12/30 at t = 110 ms.

Figure 12

Deformations and motions of three sick RBCs in a constricted vessel (d/D = 10/30) with Re = 0.4.

Figure 13

Variations of the (a) length-to-diameter and (b) width-to-diameter ratios of healthy RBCs during Poiseuille flow through microchannels with different degrees of constriction.

Figure 14

Variations of the width-to-length ratio for healthy RBCs during Poiseuille flow through microchannels with different degrees of constriction represented by d/D values of 30/30, 24/30, 20/30, 16/30, 12/30, and 10/30, respectively.

Figure 15

Variations of the length-to-radius ratio of the healthy and sick RBC II during Poiseuille flow through microchannels with different degrees of constriction represented by d/D values of 30/30, 24/30, 20/30, 16/30, 12/30, and 10/30, respectively.