3D Fluid-Structure Interaction Simulation of Aortic Valves Using a Unified Continuum ALE FEM Model

Abstract

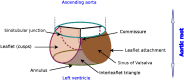
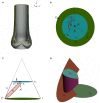
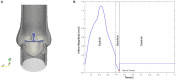
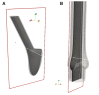
Due to advances in medical imaging, computational fluid dynamics algorithms and high performance computing, computer simulation is developing into an important tool for understanding the relationship between cardiovascular diseases and intraventricular blood flow. The field of cardiac flow simulation is challenging and highly interdisciplinary. We apply a computational framework for automated solutions of partial differential equations using Finite Element Methods where any mathematical description directly can be translated to code. This allows us to develop a cardiac model where specific properties of the heart such as fluid-structure interaction of the aortic valve can be added in a modular way without extensive efforts. In previous work, we simulated the blood flow in the left ventricle of the heart. In this paper, we extend this model by placing prototypes of both a native and a mechanical aortic valve in the outflow region of the left ventricle. Numerical simulation of the blood flow in the vicinity of the valve offers the possibility to improve the treatment of aortic valve diseases as aortic stenosis (narrowing of the valve opening) or regurgitation (leaking) and to optimize the design of prosthetic heart valves in a controlled and specific way. The fluid-structure interaction and contact problem are formulated in a unified continuum model using the conservation laws for mass and momentum and a phase function. The discretization is based on an Arbitrary Lagrangian-Eulerian space-time finite element method with streamline diffusion stabilization, and it is implemented in the open source software Unicorn which shows near optimal scaling up to thousands of cores. Computational results are presented to demonstrate the capability of our framework.

Keywords: Arbitrary Lagrangian-Eulerian method; blood flow; finite element method; fluid-structure interaction; parallel algorithm; patient specific heart model.

Figure 1

Glossary of the aortic root, author's own drawing based on Sievers et al. (2012). Annulus, leaflets, leaflet attachment, sinotubular junction, interleaflet triangle and sinus of Valsalva are the different components of the aortic root. The aortic valve consists of the three leaflets only.

Figure 2

To detect collision we calculate the distance d_ij between the leaflets L^j and Lⁱ for i, j = 1, 2, 3 (A). As soon as the minimal distance is below a certain threshold, the valve opening is closed. A 2D-surface (blue) is included to model a proper closure (B) and the geometric model of the valve opening is closed by marking the cells directly attached to the 2D-surface as solid (C).

Figure 3

A CAD model of an idealized native aortic root (A) and its parameters in top down view (B) and side view (C) are depicted. The creation of the surface of one leaflet is illustrated in (D).

Figure 4

Initial and boundary conditions for the native valve: starting configuration for the simulation (A) and the magnitude of the inflow plotted against time (B).

Figure 5

The geometry of a bileaflet mechanical heart valve. (A) Shows a typical bileaflet mechanical heart valve which is used as an artificial implant, and (B) is a simplified BMHV embedded in an idealized aorta used in our simulations.

Figure 6

All 2-D images are visualized using these 2-D cuts in Paraview (Ahrens et al., 2005). The plane for the BMHV (A) is defined by its origin in (0.278, −1.65, 1.05) and normal (0, 1, 0), and the plane for the native valve (B) by its origin in (−0.179, 0.0, 1.05) and normal (0, 1, 0).

Figure 7

The geometric orifice area is plotted against time.

Figure 8

The instantaneous vector field of the velocity using arrows and line integral convolution (LIC), the pressure field and the aortic valve position during RVOT [t = 0.05 (A), 0.08 (B), 0.1 s (C)].

Figure 9

The instantaneous vector field of the velocity using arrows and line integral convolution (LIC), the pressure field and the aortic valve position in the phases of gradual closure [t = 0.25 (A), 0.3 (B)] and RVCT [t = 0.4 s (C)].

Figure 10

A small vortex is formed at the tip of the backside of the leaflet at t = 0.25 s as the flow starts to decelerate.

Figure 11

During the phase of deceleration a boundary between the outflowing jet (A) and regions with recirculating flow (B,C) can be observed. The figures show the velocity field at t = 0.3 s.

Figure 12

Two different vortices can be located during valve closure. Velocity field at t = 0.35 s (A) and t = 0.4 s (B).

Figure 13

The von Mises Stress τ_v (Pa) is plotted at instantaneous time points during the acceleration phase, systole and deceleration phase: Leaflet position at t = 0.05 s (A), t = 0.08 s (B), t = 0.1 s (C), t = 0.3 s (D), t = 0.4 s (E), t = 0.442s (F).

Figure 14

The definition of the rotational angle α is illustrated in (A) and the simulation results of the rotational angle and velocity are plotted in (B).

Figure 15

Snapshots of the velocity field and vortex structure of a BMHV at (from left to right) t = 0.1, 0.11, 0.115, 0.120, 0.124 s: Velocity field using LIC are depicted in (A). The marked areas are enlarged and a close up view of circulations areas is shown in (B). Three-dimensional vortex structures are visualized in (C) by using the λ₂-criterion.