Complex gaze stabilization in mantis shrimp

Abstract

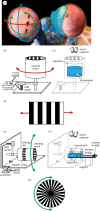
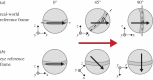
Almost all animals, regardless of the anatomy of the eyes, require some level of gaze stabilization in order to see the world clearly and without blur. For the mantis shrimp, achieving gaze stabilization is unusually challenging as their eyes have an unprecedented scope for movement in all three rotational degrees of freedom: yaw, pitch and torsion. We demonstrate that the species Odontodactylus scyllarus performs stereotypical gaze stabilization in the yaw degree of rotational freedom, which is accompanied by simultaneous changes in the pitch and torsion rotation of the eye. Surprisingly, yaw gaze stabilization performance is unaffected by both the torsional pose and the rate of torsional rotation of the eye. Further to this, we show, for the first time, a lack of a torsional gaze stabilization response in the stomatopod visual system. In the light of these findings, we suggest that the neural wide-field motion detection network in the stomatopod visual system may follow a radially symmetric organization to compensate for the potentially disorientating effects of torsional eye movements, a system likely to be unique to stomatopods.

Keywords: eye movements; gaze stabilization; neural connections; optokinesis; stomatopod.

Figure 1.

(a) Stomatopods can rotate their eyes in all three degrees of freedom: yaw (red; side-to-side), pitch (blue; up-down) and torsion (green; rotation about the stalk). Photo credit: Mike Bok. (b) The rotating drum with the black and white grating on the inner face used to elicit yaw optokinesis. (c) Individual stomatopods are placed in the stationary aquarium with their body concealed within an artificial ‘burrow’ and their exposed eyes, located at the centre of the drum, are filmed using stereoscopic cameras from above. (d) Motion of the rotating drum (b,c) creates a field of view moving in the horizontal direction. (e) The torsional rotating drum. As for (a–c), the sides of the drum were covered with a black and white grating. (f) Individual stomatopods are placed in the stationary counterbalanced aquarium in the middle of the drum and filmed from above through slits in the drum. (g) The end of the drum (left in (d,e)), directly in front of the stomatopod, was filled with a radial pattern of black and white segments, which rotated torsionally at the same rate as the drum. (Online version in colour.)

Figure 2.

(a–c) The three-dimensional rotational response (yaw (red), pitch (blue) and torsion (green)) of the left eye of a single stomatopod during three separate trials in which the striped drum rotated anticlockwise in the yaw plane, producing a horizontally moving field of view. (d) The distribution of relative velocity ratios during the fast and slow phases of yaw optokinesis across the left and right eyes of 17 O. scyllarus during presentation of the drum rotating in both directions. Dashed vertical line indicates ‘perfect’, idealized gaze stabilization (S_Y = 1). S_Y > 0 when the eye is yawing in the same direction as the drum and S_Y < 0 when yawing in the opposite direction (dark red region), as occurs during fast resets (n = 17, error bars are standard deviation across all animals in each 0.5 interval). (e) Distribution of the cross-correlation coefficients between the angular pose of each of the degrees of eye rotation during yaw-plane experiments showing non-significant correlation between yaw and torsion, yaw and pitch, and torsion and pitch for the left and right eyes (n = 17). Horizontal dashed line indicates a cross-correlation coefficient of 0. (f) Boxplot of the cross-correlation coefficients between the relative velocity ratio in the yaw degree of freedom and the torsional rotation of the left and right eyes during yaw-plane experiments. Yaw gaze stabilization performance is independent of both torsional pose and velocity of torsional rotation. Horizontal dashed line indicates a cross-correlation coefficient of 0. (g) Median values of relative velocity ratio in 10° intervals as the left (orange) and right (black) eyes rotate torsionally from horizontal (0°) to vertical (90°) (n = 17, error bars are the standard deviation across all animals in each 10°interval).

Figure 3.

(a) The yaw (red), pitch (blue) and torsion (green) rotation of a single eye from an individual elicited by the torsional rotation of the drum in the clockwise direction at the slow speed setting (3.41 ± 0.04°s⁻¹ (mean ± s.d.)). (b,c) Torsional rotation at the medium (7.48 ± 0.42°s⁻¹; clockwise) and fast (12.74 ± 0.16°s⁻¹; anticlockwise) speeds. Dotted lines (a–c) indicate the progress of the torsionally rotating drum, but do not necessarily represent specific stripe boundaries. Torsion of the eye does not show stereotypical optokinetic nystagmus. Missing regions are due to occlusion of the eyes by the support struts of the rotating drum. (d) Average angular torsional velocity of both eyes (left and right) of all six individuals (black line) increased with the angular velocity of the drum. Error bars are the standard deviation at each drum speed (n = 6). Also shown (grey) are the average angular torsional velocities of both eyes of each individual. (e–g) Distribution of relative velocity ratios during the fast and slow phases of torsional optokinesis across both eyes of six animals during clockwise and anticlockwise presentations at the (e) slow, (f) medium and (g) fast speed settings. The dashed line indicates ‘perfect’, idealized gaze stabilization, S_T = 1. As for figure 2d, counter rotation indicated by the dark green region. Error bars are the standard deviation across all animals in each 0.5 interval (n = 6). (h) Average torsional relative velocity ratios of both eyes of all six individuals (black line) at each drum speed setting all exceed S_T = 1. Error bars are the standard deviation at each drum speed (n = 6). Also shown (grey) are the average torsional relative velocity ratios of both eyes of each individual. While eye velocity approaches the drum velocity (S_T ≈ 1), gaze-stabilizing eye movements are expected to be slightly slower (S_T) than the drum movements due to the finite response time of the neural feedback loop.

Figure 4.

(a) The motion of a stimulus moving in the horizontal direction (red arrow) in the real-world coordinate system (indicated by the axes) across a stomatopod's eye depends on its torsional pose. (b) In its reference frame, rather than an eye torsionally rotating, it remains motionless with the midband fixed in the horizontal position, while the world rotates torsionally about the eye, as shown by the orientation of the real-world coordinate axes. In the eye's reference frame, the apparent direction of motion of the stimulus moving horizontally in the real world depends on its torsional pose. Despite the ubiquitous torsional rotations observed during yaw tracking causing a dynamic apparent direction of motion, stomatopods are able to accurately track the actual motion of a horizontally displaced field of view, showing normal optokinetic nystagmus in the yaw rotation, despite simultaneous (but uncorrelated) pitch and torsion rotations. (Online version in colour.)