Experimental two-dimensional quantum walk on a photonic chip

Abstract

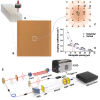
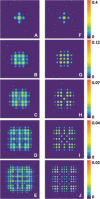
Quantum walks, in virtue of the coherent superposition and quantum interference, have exponential superiority over their classical counterpart in applications of quantum searching and quantum simulation. The quantum-enhanced power is highly related to the state space of quantum walks, which can be expanded by enlarging the photon number and/or the dimensions of the evolution network, but the former is considerably challenging due to probabilistic generation of single photons and multiplicative loss. We demonstrate a two-dimensional continuous-time quantum walk by using the external geometry of photonic waveguide arrays, rather than the inner degree of freedoms of photons. Using femtosecond laser direct writing, we construct a large-scale three-dimensional structure that forms a two-dimensional lattice with up to 49 × 49 nodes on a photonic chip. We demonstrate spatial two-dimensional quantum walks using heralded single photons and single photon-level imaging. We analyze the quantum transport properties via observing the ballistic evolution pattern and the variance profile, which agree well with simulation results. We further reveal the transient nature that is the unique feature for quantum walks of beyond one dimension. An architecture that allows a quantum walk to freely evolve in all directions and at a large scale, combining with defect and disorder control, may bring up powerful and versatile quantum walk machines for classically intractable problems.

Fig. 1. Experimental layout.

(A) Schematic diagram of 3D waveguide array fabrication using the femtosecond laser direct writing technique. (B) Photographed cross section of a photonic lattice studied in this experiment. (C) Schematic diagram of one waveguide coupling to other waveguides in the 3D waveguide arrays, and (D) the corresponding coupling coefficient C for different center-to-center waveguide spacings in horizontal and vertical directions. (E) Setup of single-photon experiment. Each photonic chip to be tested incorporates many sets of 3D waveguide arrays. APD, avalanched photo diode; PBS, polarized beam splitter; HWP, half-wave plate; QWP, quarter-wave plate; LPF, long-pass filter; PPKTP, periodically poled KTP crystal.

Fig. 2. 2D QWs of different propagation lengths.

(A to E) Experimentally obtained probability distribution of heralded single photons and (F to J) theoretical probability distribution. The propagation lengths are 1.81 mm for (A) and (F), 3.31 mm for (B) and (G), 4.81 mm for (C) and (H), 7.31 mm for (D) and (I), and 9.81 mm for (E) and (J).

Fig. 3. The transport properties of QWs.

(A) The variance against propagation length for experimental 2D QWs, theoretical 2D QWs, and theoretical 1D QWs. a.u., arbitrary units. (B) An evolution pattern of a 2D QW from heralded single-photon experiment at a propagation length z = 4.31 mm and its projection profile onto the x and y axes. (C) A theoretical evolution pattern of a 2D classical random walk in a 2D Gaussian distribution with a sigma of 1.5 spacing units and its projection profile onto the x and y axes.

Fig. 4. The recurrent properties.

(A) Probability at the initial position against propagation length and (B) Pólya number against propagation length for experimental 2D QWs, theoretical 2D QWs, and theoretical 1D QWs.