A paradox of epidemics between the state and parameter spaces

Abstract

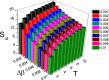
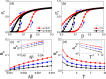
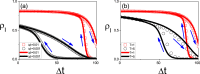
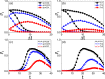
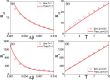
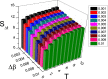
It is recently revealed from amounts of real data of recurrent epidemics that there is a phenomenon of hysteresis loop in the state space. To understand it, an indirect investigation from the parameter space has been given to qualitatively explain its mechanism but a more convincing study to quantitatively explain the phenomenon directly from the state space is still missing. We here study this phenomenon directly from the state space and find that there is a positive correlation between the size of outbreak and the size of hysteresis loop, implying that the hysteresis is a nature feature of epidemic outbreak in real case. Moreover, we surprisingly find a paradox on the dependence of the size of hysteresis loop on the two parameters of the infectious rate increment and the transient time, i.e. contradictory behaviors between the two spaces, when the evolutionary time of epidemics is long enough. That is, with the increase of the infectious rate increment, the size of hysteresis loop will decrease in the state space but increase in the parameter space. While with the increase of the transient time, the size of hysteresis loop will increase in the state space but decrease in the parameter space. Furthermore, we find that this paradox will disappear when the evolutionary time of epidemics is limited in a fixed period. Some theoretical analysis are presented to both the paradox and other numerical results.

Figure 1

A typical real data of recurrent epidemics and its features. (a) Represents the time series of reported measles infective cases I in New York, where the variable I is from 0 to 3 × 10⁴. (b) Amplification of the outbreak marked in the blue circle of (a). (c) The hysteresis loop of (b) in the rescaled framework where the original point is taken as the time pointed by the dashed line in (b) and the “squares” and “circles” denote the growing and recovering phases, respectively. (d) The area S_t of each outbreak in (a) where t_n is the number of outbreaks. (e) The area S_Δt of hysteresis loops for the successive outbreaks in (a).

Figure 2

Hysteresis loops in state space where the arrows denote the evolutionary directions. (a) ρ_I versus Δt for fixed T = 1 where the curves with “squares” and “circles” represent the cases of Δβ = 0.01 and 0.001, respectively. (b) ρ_I versus Δt for fixed Δβ = 0.01 where the curves with “squares” and “circles” represent the cases of T = 1 and 5, respectively. (c) S_Δt versus Δβ where the curves with “squares”, “circles” and “triangles” represent the cases of T = 1, 2 and 3, respectively. The inset shows the log-log plot. (d) S_Δt versus T where the curves with “squares”, “circles” and “triangles” represent the cases of Δβ = 0.02, 0.01 and 0.005, respectively. The inset shows the log-log plot.

Figure 3

3D plot of the dependence of S_Δt on the two parameters Δβ and T where the other parameters are the same as in Fig. 2(c) and (d).

Figure 4

The relationship between Δβ and T for fixed S_Δt where the curves with “squares”, “circles” and “triangles” represent the cases of S_Δt = 14.0, 14.5 and 15.0, respectively.

Figure 5

Hysteresis loops in parameter space where (a–d) corresponds to Fig. 2(a–d), respectively.

Figure 6

Consistence between the state and parameter spaces where the “squares” and “circles” in (a) and (b) come from Fig. 5(a) and (b) by Eq. (3), respectively, and the solid lines in (a) and (b) are the replotted Fig. 2(a) and (b), respectively.

Figure 7

Case of fixed total evolutionary time as 2 × 20 (20 for the growing process and 20 for the recovering process) where all the parameters in (a) and (c) are the same as in Fig. 2(a) and that in (b) and (d) are the same as in Fig. 2(b). (a) and (b) represent the cases of S_Δt for fixed Δβ and fixed T, respectively. (c) and (d) represent the cases of S_t corresponding to (a) and (b), respectively.

Figure 8

(a) and (b) represent the dependence of S_Δt on the two parameters Δβ and T in state space, respectively, where the “squares” denote the numerical simulations and the solid lines are the theoretical results from Eqs (11) and (16). (c) and (d) represent the corresponding S_t of (a) and (b) in state space, respectively, where the “squares” denote the numerical simulations and the solid lines are the theoretical results from Eqs (11) and (16). The other parameters are the same as in Fig. 2(c) and (d).

Figure 9

Hysteresis loops in state space for the case of SF network. (a) ρ_I versus Δt for fixed T = 1 where the curves with “squares” and “circles” represent the cases of Δβ = 0.01 and 0.001, respectively. (b) ρ_I versus Δt for fixed Δβ = 0.01 where the curves with “squares” and “circles” represent the cases of T = 1 and 5, respectively. (c) S_Δt versus Δβ where the curves with “squares”, “circles” and “triangles” represent the cases of T = 1, 2 and 3, respectively. The inset shows the log-log plot. (d) S_Δt versus T where the curves with “squares”, “circles” and “triangles” represent the cases of Δβ = 0.02, 0.01 and 0.005, respectively. The inset shows the log-log plot.

Figure 10

3D plot of the dependence of S_Δt on the two parameters Δβ and T for the case of SF network where the other parameters are the same as in Fig. 9(c) and (d).