Fatigue-life distributions for reaction time data

Abstract

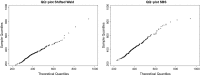
The family of fatigue-life distributions is introduced as an alternative model of reaction time data. This family includes the shifted Wald distribution and a shifted version of the Birnbaum-Saunders distribution. Although the former has been proposed as a way to model reaction time data, the latter has not. Hence, we provide theoretical, mathematical and practical arguments in support of the shifted Birnbaum-Saunders as a suitable model of simple reaction times and associated cognitive mechanisms.

Keywords: Birnbaum–Saunders distribution; Fatigue-life distributions; Latent cognitive processes; Reaction times; Shifted Wald distribution.

Fig. 1

Different BS PDFs according to different parametrization. In red $\alpha =0.5\text{and}\beta =1$; in green $\alpha =0.8\text{and}\beta =1$; in blue $\alpha =1.5\text{and}\beta =1$; and in cyan $\alpha =0.2\text{and}\beta =1.5$. We can notice that in the last case, $\alpha$ is small, and then its shape is more symmetrical than the former cases. This is because its expectation, $\beta (1+{\alpha }^2/2)$ is near its median $\beta$. (Color figure online)

Fig. 2

QQ plots of SW and SBS distributions for DS1 (from left to right), whose coefficients of determination were $\approx 0.99$ in both cases. This shows that the SBS can also be considered as a good candidate to fit RT data. According to the parametrization shown in (6), the maximum likelihood estimators were $\widehat{\alpha }\approx 0.54,\widehat{\beta }\approx 222.03$ and $\widehat{\theta }\approx 542$

Fig. 3

QQ plots of SW and SBS distributions for DS2 (from left to right), whose coefficients of determination were $\approx 0.98$ and $\approx 0.99$, respectively. Again, this shows that the SBS can also be considered as a good candidate to fit RT data. For this case, the maximum likelihood estimators were $\widehat{\alpha }\approx 0.60,\widehat{\beta }\approx 215.88$ and $\widehat{\theta }\approx 493$

Fig. 4

QQ plots of SW and SBS distributions for DS3 (from left to right), whose coefficients of determination were $\approx 0.99$ in both cases. This shows again the good performance of the SBS to describe RT data. According to the parametrization shown in (6), the maximum likelihood estimators were $\widehat{\alpha }\approx 0.57,\widehat{\beta }\approx 175$ and $\widehat{\theta }\approx 217$

Fig. 5

QQ plots of SW and SBS distributions for DS4 (from left to right), whose coefficients of determination were $\approx 0.99$ in both cases. Again, the good performance of the SBS for RT data is demonstrated. For this case, the maximum likelihood estimators were $\widehat{\alpha }\approx 0.5,\widehat{\beta }\approx 200.35$ and $\widehat{\theta }\approx 186.15$