Filter-Based Phase Shifts Distort Neuronal Timing Information

Abstract

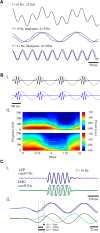
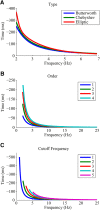
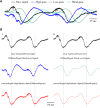
Filters are widely used for the modulation, typically attenuation, of amplitudes of different frequencies within neurophysiological signals. Filters, however, also induce changes in the phases of different frequencies whose amplitude is unmodulated. These phase shifts cause time lags in the filtered signals, leading to a disruption of the timing information between different frequencies within the same signal and between different signals. The emerging time lags can be either constant in the case of linear phase (LP) filters or vary as a function of the frequency in the more common case of non-LP (NLP) filters. Since filters are used ubiquitously online in the early stages of data acquisition, the vast majority of neurophysiological signals thus suffer from distortion of the timing information even prior to their sampling. This distortion is often exacerbated by further multiple offline filtering stages of the sampled signal. The distortion of timing information may cause misinterpretation of the results and lead to erroneous conclusions. Here we present a variety of typical examples of filter-induced phase distortions and discuss the evaluation and restoration of the timing information underlying the original signal.

Keywords: filters; neurophysiology; oscillations; phase; timing; waveform.

Graphical abstract

Figure 1.

Filter induced magnitude and phase changes in the signal. The changes induced by a 2-Hz high-pass four-pole Butterworth filter. A, Differential effect on four sinusoidal signals (black –raw signal and blue-filtered signal). B, The amplification and phase change in the signals following the filtering. C, The amplitude (top), phase (middle), and temporal (bottom) responses of the filter over all frequencies.

Figure 2.

Filter-induced phase shifts of low frequencies. A, Differential effect of filtering on the phase of the LFP (5 Hz) and action potentials (1000 Hz; cutoff frequency: 2 Hz). B, Filter induced phase shifts leading to changes the timing and wave form of the filtered signal in relation to an external event (cutoff frequency: 2 Hz). Black-raw signal and blue–filtered signal.

Figure 3.

Differential phase shifts of different frequencies. Phase changes induced by a high-pass four-pole Butterworth filter in different examples (black, raw signal; blue, filtered signal). A, Time shifts induced by narrow band filters in the θ (top) and β (bottom) bands, overlaid on the original oscillations constituting the signal. B, Effects of secondary filtration on coupling of θ and γ band oscillations. Traces (i) of coupled θ (4 Hz) and γ (40 Hz) band oscillations, before (top) and after (bottom) filtration (3–20 Hz and 30–80 Hz two-poles Butterworth filters, respectively). Spectrograms (ii) of the γ band frequency phase locked to the θ wave, before (top) and after (bottom) filtration. C, The effects of different filters on identical signals originating from different sources (i): LFP (top) and EMG (bottom; cutoff frequencies: 1 Hz, filtered LFP signal, blue; 7 Hz, filtered EMG signal, green); (ii) dashed black vertical lines mark the initiation of the oscillatory event, identified by threshold (mean ± SD of noise) crossing (right, raw; middle and left, 1- and 7-Hz high-pass-filtered signal, respectively).

Figure 4.

Effects of filter design on time shifts. The effects of (A) the filter type (Butterworth, Chebyshev and elliptic filters), (B) the filter order (one to four poles), (C) and the cutoff frequency (1–5 Hz) on filter induced time shifts.

Figure 5.

Effects of different filter designs and phase correction of an extracellularly recorded electrophysiological signal. A, The effects of high (blue, cutoff frequency: 4 Hz), low (green, cutoff frequency: 20 Hz), and band (cyan, pass-band: 4–20 Hz) pass four-poles Butterworth filters on an extracellular signal recorded from a rat striatum (black). B, Phase correction (red) by refiltering of the reversed filtered (i) high-pass and (ii) low-pass signals using similar filter designs.