Vector polymorphic beam

Abstract

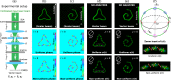
A scalar polymorphic beam is designed with independent control of its intensity and phase along a strongly focused laser curve of arbitrary shape. This kind of beam has been found crucial in the creation of freestyle laser traps able to confine and drive the motion of micro/nano-particles along reconfigurable 3D trajectories in real time. Here, we present and experimentally prove the concept of vector polymorphic beam adding the benefit of independent design of the light polarization along arbitrary curves. In particular, we consider polarization shaped tangential and orthogonal to the curve that are of high interest in optical manipulation and laser micromachining. The vector polymorphic beam is described by a surprisingly simple closed-form expression and can be easily generated by using a computer generated hologram.

Figure 1

(a) Sketch of the system used for the generation and analysis of vector beams. (b) Intensity and phase distributions of a scalar polymorphic beam shaped in form of triangular-like curve given by Eq. (9) with parameters q = (1, 1.8, 1, 2, 1.4, 6) and ρ(t) = constant. The second and third rows show the uniform and non-uniform phase distributions (charge l = 8) prescribed along the curve. (c) Intensity and phase shaped along a spiral curve with q = (1, 1, 250, 100, 100, 6) and ρ(t) ∝ t. (d,e) Experimental results: vector polymorphic beam with uniform and non-uniform polarization variation, $\mathbf{e}(t)=(e^{\mathrm{i}2p\pi \sigma (t)},e^{-\mathrm{i}2p\pi \sigma (t)})/\sqrt{2}$, prescribed along the curve. In the experiments the focal length is f = 150 mm and the input collimated laser beam (linear polarized) has a wavelength of λ = 532 nm. (f) Changes of the polarization state along the curved vector beams considered in this example. The repetitive changes of the polarization, associated with the movements on the green-marked meridians of the Poincaré sphere, along the curves are illustrated in the corresponding zoom inserts of (d).

Figure 2

Experimental results: intensity distributions of a vector polymorphic beam ${\tilde{E}}_1(u,v){\mathbf{e}}_1+{\tilde{E}}_2(u,v){\mathbf{e}}_2$ with a polarization set tangential to the curve. In this case an uniform phase distribution (l = 8), e₁ = (1, 0) and e₂ = (0, 1) have been used. The first row displays the intensity distribution of the generated vector beams while the second and third ones shown their intensities when an analyzer is rotated, see also Supplementary Video 1. The last row shows that the polarization is linear in all the points of the curve and forms an angle θ = (arctan(S₂/S₁))/2 with horizontal axis, where S_1,2 are measured Stokes parameters. The polarization is tangential to the curve as expected. Curve parameters: (a) triangular-like curve q = (1, 1.8, 1, 2, 1.4, 6), (b) spiral q = (1, 1, 250, 100, 100, 6) with ρ(t) ∝ t, (c) a polygon with q = (2.7, 2.6, 6, 12, 8.3, 5.3), starfish curve q = (10, 10, 2, 7, 7, 5), spiral with q = (1, 1, 5, 5, 5, 10) and ρ(t) ∝ t^0.2.