Reconstruction of antibody dynamics and infection histories to evaluate dengue risk
- PMID: 29795354
- PMCID: PMC6064976
- DOI: 10.1038/s41586-018-0157-4
Reconstruction of antibody dynamics and infection histories to evaluate dengue risk
Abstract
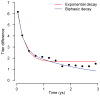
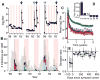
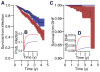
As with many pathogens, most dengue infections are subclinical and therefore unobserved 1 . Coupled with limited understanding of the dynamic behaviour of potential serological markers of infection, this observational problem has wide-ranging implications, including hampering our understanding of individual- and population-level correlates of infection and disease risk and how these change over time, between assay interpretations and with cohort design. Here we develop a framework that simultaneously characterizes antibody dynamics and identifies subclinical infections via Bayesian augmentation from detailed cohort data (3,451 individuals with blood draws every 91 days, 143,548 haemagglutination inhibition assay titre measurements)2,3. We identify 1,149 infections (95% confidence interval, 1,135-1,163) that were not detected by active surveillance and estimate that 65% of infections are subclinical. After infection, individuals develop a stable set point antibody load after one year that places them within or outside a risk window. Individuals with pre-existing titres of ≤1:40 develop haemorrhagic fever 7.4 (95% confidence interval, 2.5-8.2) times more often than naive individuals compared to 0.0 times for individuals with titres >1:40 (95% confidence interval: 0.0-1.3). Plaque reduction neutralization test titres ≤1:100 were similarly associated with severe disease. Across the population, variability in the size of epidemics results in large-scale temporal changes in infection and disease risk that correlate poorly with age.
Conflict of interest statement
The authors declare no competing financial interests or competing interests.
Figures
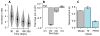
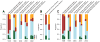
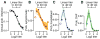
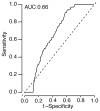
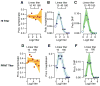


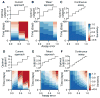
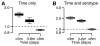


Comment in
-
Detecting dengue.Nat Med. 2018 Jul;24(7):898. doi: 10.1038/s41591-018-0120-9. Nat Med. 2018. PMID: 29988137 No abstract available.
References
-
- Endy TP, et al. Epidemiology of inapparent and symptomatic acute dengue virus infection: a prospective study of primary school children in Kamphaeng Phet, Thailand. American Journal of Epidemiology. 2002;156:40–51. - PubMed
-
- Halstead SB. Dengue. Imperial College Press; London: 2008.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Research Materials

