Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2015 Apr;75(2):185-207.
doi: 10.1177/0013164414534258. Epub 2014 May 16.

Real and Artificial Differential Item Functioning in Polytomous Items

David Andrich  1 , Curt Hagquist  2
Affiliations

Real and Artificial Differential Item Functioning in Polytomous Items

David Andrich et al. Educ Psychol Meas. 2015 Apr.

Abstract

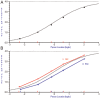
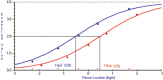
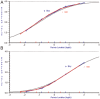
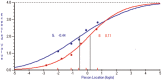
Differential item functioning (DIF) for an item between two groups is present if, for the same person location on a variable, persons from different groups have different expected values for their responses. Applying only to dichotomously scored items in the popular Mantel-Haenszel (MH) method for detecting DIF in which persons are classified by their total scores on an instrument, Andrich and Hagquist articulated the concept of artificial DIF and showed that as an artifact of the MH method, real DIF in one item favoring one group inevitably induces artificial DIF favoring the other group in all other items. Using the dichotomous Rasch model in which the total score for a person is a sufficient statistic, and therefore justifies classifying persons by their total scores, Andrich and Hagquist showed that to distinguish between real and artificial DIF in an item identified by the MH method, a sequential procedure for resolving items is implied. Using the polytomous Rasch model, this article generalizes the concept of artificial DIF to polytomous items, in which multiple item parameters play a role. The article shows that the same principle of resolving items sequentially as with dichotomous items applies also to distinguishing between real and artificial DIF with polytomous items. A real example and a small simulated example that parallels the real example are used illustratively.

Keywords: artificial DIF; differential item functioning; partial credit; polytomous Rasch model; rating scales.

PubMed Disclaimer

Conflict of interest statement

Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Figures

Figure 1.
Figure 1.
Theoretical ICCs for Item 1 and observed means (•) in five class intervals in the example with three items: (A) Groups aggregated; (B) Groups disaggregated.
Figure 2.
Figure 2.
Theoretical ICCs and observed means (•) in five class intervals for Items 2 and 3 in the example with three items showing artificial DIF: (A) Item 2: boys and girls aggregated; (B) Item 3: boys and girls disaggregated.
Figure 3.
Figure 3.
Theoretical ICCs for resolved Item 1 and observed means (•) in five class intervals in the example with three items.
Figure 4.
Figure 4.
Theoretical ICCs and observed means (•) in five class intervals for Items 2 and 3 in the example with three items when Item 1 is resolved: (A) Item 2: boys and girls disaggregated; (B) Item 3: boys and girls disaggregated.
Figure 5.
Figure 5.
ICCs for resolved Item 7 and observed means (•) in five class intervals.
Figure 6.
Figure 6.
Person and threshold distributions with Items 7 and 4 resolved.
See this image and copyright information in PMC

References

    1. Andersen E. B. (1977). Sufficient statistics and latent trait models. Psychometrika, 42, 69-81.
    1. Andrich D. (1978). A rating formulation for ordered response categories. Psychometrika, 43, 561-574.
    1. Andrich D., Hagquist C. (2012). Real and artificial differential item functioning. Journal of Educational and Behavioral Statistics, 37, 387-416. - PMC - PubMed
    1. Andrich D., Luo G. (2003). Conditional estimation in the Rasch model for ordered response categories using principal components. Journal of Applied Measurement, 4, 205-221. - PubMed
    1. Andrich D., Sheridan B., Luo G. (2013). RUMM2030: A Windows interactive program for analysing data with Rasch unidimensional model for measurement. Perth, Western Australia, Australia: RUMM Laboratory.

LinkOut - more resources