Descriptive Statistics for Modern Test Score Distributions: Skewness, Kurtosis, Discreteness, and Ceiling Effects

Abstract

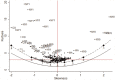
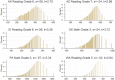
Many statistical analyses benefit from the assumption that unconditional or conditional distributions are continuous and normal. More than 50 years ago in this journal, Lord and Cook chronicled departures from normality in educational tests, and Micerri similarly showed that the normality assumption is met rarely in educational and psychological practice. In this article, the authors extend these previous analyses to state-level educational test score distributions that are an increasingly common target of high-stakes analysis and interpretation. Among 504 scale-score and raw-score distributions from state testing programs from recent years, nonnormal distributions are common and are often associated with particular state programs. The authors explain how scaling procedures from item response theory lead to nonnormal distributions as well as unusual patterns of discreteness. The authors recommend that distributional descriptive statistics be calculated routinely to inform model selection for large-scale test score data, and they illustrate consequences of nonnormality using sensitivity studies that compare baseline results to those from normalized score scales.

Keywords: accountability; descriptive statistics; exploratory data analysis; high-stakes testing; psychometrics.

Figure 1.

Skewness and kurtosis of raw score (gray, n = 174) and scale score (black, n = 330) distributions from 14 state testing programs, Grades 3 to 8, reading and mathematics, 2010 and 2011. Note. Distributions with kurtosis >5 are labeled with their state abbreviations: CO = Colorado; NY0 = New York, 2010; NY1 = New York, 2011; OK = Oklahoma; PA = Pennsylvania; WA = Washington. The theoretical lower bound of skewness and kurtosis is shown as a solid curve. The skewness and kurtosis of beta-binomial distributions are shown as a dashed line as a function of the average item proportion correct, µ_p, under the constraint that the test comprises 50 dichotomously scored items with item difficulties distributed as a beta distribution with parameters α and β that sum to 4.

Figure 2.

Skewness and kurtosis of scale score distributions from 14 state testing programs, Grades 3 to 8, reading and mathematics, 2010 and 2011, shown as boxplots by state abbreviations. Note. States are abbreviated. AK = Alaska; AZ = Arizona; CO = Colorado; ID = Idaho; NE = Nebraska; 4S = New England Common Assessment Program (Maine, New Hampshire, Rhode Island, Vermont); NJ = New Jersey; NY0 = New York, 2010; NY1 = New York, 2011; NC = North Carolina; OK = Oklahoma; PA = Pennsylvania; SD = South Dakota; TX = Texas; WA = Washington.

Figure 3.

Six discrete histograms of scale scores selected from a pool of 46 symmetric, mesokurtic distributions with skewness between ±0.1 and kurtosis between 2.75 and 3.75. Distributions chosen to illustrate characteristically stretched, high-density upper tails in spite of near-zero skewness. Note. All distributions are from 2011. s = skewness; k = kurtosis.

Figure 4.

Upper-tail features of scale score distributions from 14 state testing programs, Grades 3 to 8, reading and mathematics, 2010 and 2011. Note. Top tile: Count of discrete score points distinguishing among the top 10% of examinees. Middle tile: Percentage of total discrete score points distinguishing among the top 10% of examinees. Bottom tile: Distance from the second highest score point to the highest score point in standard deviation units. States are abbreviated. AK = Alaska; AZ = Arizona; CO = Colorado; ID = Idaho; NE = Nebraska; 4S = New England Common Assessment Program (Maine, New Hampshire, Rhode Island, Vermont); NJ = New Jersey; NY0 = New York, 2010; NY1 = New York, 2011; NC = North Carolina; OK = Oklahoma; PA = Pennsylvania; SD = South Dakota; TX = Texas; WA = Washington.