Detecting change in stochastic sound sequences

Abstract

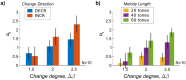
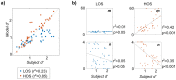
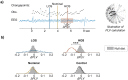
Our ability to parse our acoustic environment relies on the brain's capacity to extract statistical regularities from surrounding sounds. Previous work in regularity extraction has predominantly focused on the brain's sensitivity to predictable patterns in sound sequences. However, natural sound environments are rarely completely predictable, often containing some level of randomness, yet the brain is able to effectively interpret its surroundings by extracting useful information from stochastic sounds. It has been previously shown that the brain is sensitive to the marginal lower-order statistics of sound sequences (i.e., mean and variance). In this work, we investigate the brain's sensitivity to higher-order statistics describing temporal dependencies between sound events through a series of change detection experiments, where listeners are asked to detect changes in randomness in the pitch of tone sequences. Behavioral data indicate listeners collect statistical estimates to process incoming sounds, and a perceptual model based on Bayesian inference shows a capacity in the brain to track higher-order statistics. Further analysis of individual subjects' behavior indicates an important role of perceptual constraints in listeners' ability to track these sensory statistics with high fidelity. In addition, the inference model facilitates analysis of neural electroencephalography (EEG) responses, anchoring the analysis relative to the statistics of each stochastic stimulus. This reveals both a deviance response and a change-related disruption in phase of the stimulus-locked response that follow the higher-order statistics. These results shed light on the brain's ability to process stochastic sound sequences.

Fig 1. Examples of random fractal melodies.

Schematic spectrograms shown with frequency and time along the vertical and horizontal axes, respectively (see S1–S6 Audio. for accompanying audio). a) Melodies at four levels of entropy, parameterized by β. Higher β corresponds with lower entropy, and vice versa. b) Change stimuli for each change direction; INCR and DECR stimuli always end and begin, respectively, with the highest level of entropy (β = 0 or white noise).

Fig 2. Psychophysics results from Experiments 1 and 2.

Average change detection performance (d′) across subjects is shown by stimulus condition. Error bars indicate 95% bootstrap confidence interval across subjects. a) In Experiment 1 (N = 10), melody entropy changed with different degrees (Δβ, abscissa) and in both INCR and DECR direction (color). Detection performance increased with Δβ but did not differ by direction, although there was a weak interaction between Δβ and direction due to FAs only (see S1 Fig). b) In Experiment 2 (N = 10), an additional factor of melody length was introduced (color). Detection performance increased with both Δβ and melody length.

Fig 3. Schematic of perceptual model and model outputs.

a) At time t, the model contains multiple parameter estimates, ${\widehat{\theta }}_t^{(.)}$, collected over run-lengths from 0 up to the memory constraint m. Each estimate yields a prediction for the next observation, with increased uncertainty due to observation noise n. Upon observing x_t+1, the model updates the run-length beliefs using the predictive probability for each hypothesis. Note that the prediction for length m is used to update all beliefs with length greater than or equal to m, thus limiting the number of past observations used in the update. A new belief with length 0 is added with probability π, the change-prior. Finally, parameter estimates are updated with x_t+1; these are in turn used to predict the next observation. b) Outputs from the model for an example change stimulus (top, foreground). At each time, the predictive distribution (top, background) combines predictions across run-length hypotheses weighted by their beliefs, thus “integrating out” run-length. Surprisal (middle) measures how well each new observation fits the prediction. The change probability (bottom) is the probability at least one changepoint has occurred, as inferred using the run-length beliefs. The model detects a change if the change probability exceeds the threshold τ. Model parameters (m, n, π, τ) are in red.

Fig 4. Range of model behavior in Experiment 1.

Model detection performance measured at different operating points in a parameter sweep. a) Comparison of detection performance for LOS and HOS models displayed in ROC-space across the parameter sweep, with model type denoted by color. Each blue (red) coordinate indicates existence of a parameter set for the LOS (HOS) model yielding that performance. Individual human performance from Experiments 1 and 1b is overlaid, along with equal-d′ curves. b) d′ surface as a function of memory (m) and observation noise (n) parameters for LOS model (top) and HOS model (bottom). π and τ were held constant at 0.01 and 0.5, respectively.

Fig 5. Model fit to subject behavior from Experiments 1–2.

a) Subject d′ plotted against fitted model d′ for both LOS and HOS models, denoted by color. Legend shows r²-value from zero-intercept linear regression. b) Fitted perceptual parameters plotted against subject d′ for m (top) and n (bottom), with LOS model on the left and HOS model on the right. r² and p-values shown for standard linear regression.

Fig 6. Contextual effects on tone ERP.

a) Grand-average ERPs (top) for large and small ΔF in LOW and HIGH entropy melodies show a positivity for large ΔF in LOW entropy context around 200ms after tone onset. Mean amplitudes are shown for ① and ② time windows (bottom). Scalp map (right) shows frontal distribution of t-test p-values for large ΔF deflection between entropy contexts. b) Using model surprisal, regression-ERP analysis teases out distinct components depending on the set of statistics used in the model: a positivity 150-230ms after onset with LOS surprisal (similar to a) above) and a MMN-like negativity 100-200ms after onset with HOS surprisal. Error bars show 95% bootstrap confidence interval across subjects.

Fig 7. Phase-locking analysis at model changepoints.

ΔPLV is used to measure disruptions in phase-locking of EEG to the tone presentation rate (6.25 Hz) at the time when the model detects a change in the stimulus (i.e., at the changepoint). a) Illustration of ΔPLV calculation. PLV measures phase agreement across trials independent of power; an example PLV calculation (right) shows the phase of individual EEG trials (in grey)—PLV is the magnitude of the mean of these normalized phasors (in black). ΔPLV is then the difference in PLV within a 7-tone (1-sec) window before and after the changepoint (left, shown at the HOS changepoint in the melody). For each subject, ΔPLV was calculated for three sets of changepoints: the changepoints output from the LOS and HOS models, and the nominal changepoint (i.e., midpoint) used to generate the stimuli. Additionally, as a control, the same HOS changepoints were applied to responses to no-change stimuli. b) Empirical distributions of ΔPLV at the LOS-, HOS-, Nominal-, and Control-changepoints (line) calculated by bootstrap sampling across subjects, along with the null distribution (solid gray) calculated by performing the same analysis with random sampling of the changepoint position. This null distribution estimates variability in ΔPLV present throughout the melody. Significant change from zero and from the null distribution is seen in the HOS-changepoint only.