From genome-wide associations to candidate causal variants by statistical fine-mapping
- PMID: 29844615
- PMCID: PMC6050137
- DOI: 10.1038/s41576-018-0016-z
From genome-wide associations to candidate causal variants by statistical fine-mapping
Abstract
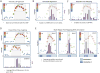
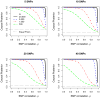
Advancing from statistical associations of complex traits with genetic markers to understanding the functional genetic variants that influence traits is often a complex process. Fine-mapping can select and prioritize genetic variants for further study, yet the multitude of analytical strategies and study designs makes it challenging to choose an optimal approach. We review the strengths and weaknesses of different fine-mapping approaches, emphasizing the main factors that affect performance. Topics include interpreting results from genome-wide association studies (GWAS), the role of linkage disequilibrium, statistical fine-mapping approaches, trans-ethnic studies, genomic annotation and data integration, and other analysis and design issues.
Conflict of interest statement
Figures


References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

