Exploring patterns enriched in a dataset with contrastive principal component analysis
- PMID: 29849030
- PMCID: PMC5976774
- DOI: 10.1038/s41467-018-04608-8
Exploring patterns enriched in a dataset with contrastive principal component analysis
Abstract
Visualization and exploration of high-dimensional data is a ubiquitous challenge across disciplines. Widely used techniques such as principal component analysis (PCA) aim to identify dominant trends in one dataset. However, in many settings we have datasets collected under different conditions, e.g., a treatment and a control experiment, and we are interested in visualizing and exploring patterns that are specific to one dataset. This paper proposes a method, contrastive principal component analysis (cPCA), which identifies low-dimensional structures that are enriched in a dataset relative to comparison data. In a wide variety of experiments, we demonstrate that cPCA with a background dataset enables us to visualize dataset-specific patterns missed by PCA and other standard methods. We further provide a geometric interpretation of cPCA and strong mathematical guarantees. An implementation of cPCA is publicly available, and can be used for exploratory data analysis in many applications where PCA is currently used.
Conflict of interest statement
The authors declare no competing interests.
Figures
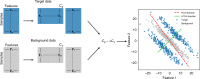
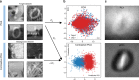
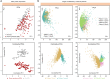
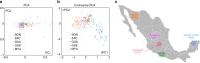
Comment in
-
Contrasting PCA across datasets.Nat Methods. 2018 Aug;15(8):572. doi: 10.1038/s41592-018-0093-0. Nat Methods. 2018. PMID: 30065385 No abstract available.
References
-
- Hotelling H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933;24:417. doi: 10.1037/h0071325. - DOI
-
- Jolliffe, I. T (ed.). Principal Component Analysis, 115–128 (Springer, New York, NY, 1986).
-
- Maaten L, Hinton G. Visualizing data using t-sne. J. Mach. Learn. Res. 2008;9:2579–2605.
-
- Cox, M. A. & Cox, T. F. Multidimensional Scaling. Handbook of Data Visualization 315–347 (Springer, Berlin, 2008).
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

