Stability of hand force production. II. Ascending and descending synergies

Abstract

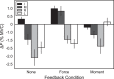
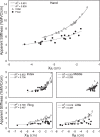
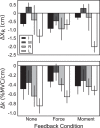
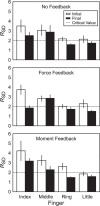
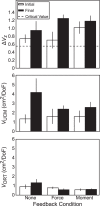
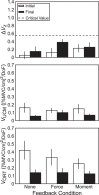
We combined the theory of neural control of movement with referent coordinates and the uncontrolled manifold hypothesis to investigate multifinger coordination. We tested hypotheses related to stabilization of performance by covarying control variables, translated into apparent stiffness and referent coordinate, at different levels of an assumed hierarchy of control. Subjects produced an accurate combination of total force and total moment of force with the four fingers under visual feedback on both variables and after feedback was partly or completely removed. The "inverse piano" device was used to estimate control variables. We observed strong synergies in the space of hypothetical control variables that stabilized total force and moment of force, as well as weaker synergies stabilizing individual finger forces; whereas the former were attenuated by alteration of visual feedback, the latter were much less affected. In addition, we investigated the organization of "ascending synergies" stabilizing task-level control variables by covaried adjustments of finger-level control variables. We observed intertrial covariation of individual fingers' referent coordinates that stabilized hand-level referent coordinate, but we observed no such covariation for apparent stiffness. The observations suggest the existence of both descending and ascending synergies in a hierarchical control system. They confirm a trade-off between synergies at different levels of control and corroborate the hypothesis on specialization of different fingers for the control of force and moment. The results provide strong evidence for the importance of central back-coupling loops in ensuring stability of action. NEW & NOTEWORTHY We expand analysis of action in the space of hypothetical control variables to hierarchically organized multieffector systems. We also introduce the novel concept of ascending synergies, which reflect covariation of control variables to individual effectors (fingers) that stabilize task-specific control variables at a hierarchically higher, task-specific level (hand).

Keywords: force; multifinger coordination; referent coordinate; synergy; uncontrolled manifold hypothesis.

Fig. 1.

A hypothetical scheme of the neural control of the four-finger total force (F_TOT) production task with referent coordinates for the effectors. At level 1, two variables R_HAND and C_HAND, are specified, based on the desired F_TOT. At level 2, these variables result in the {R_f; C_f} pairs for the individual fingers, f = I (index), M (middle), R (ring), and L (little). At level 3, individual finger forces F_f are produced by the corresponding {R_f; C_f} pairs. At level 4, the finger forces sum up to produce hand force, F_HAND. At each level, pairs of variables computed from experimental data {X_R; k} are used as proxies for the control pairs R and C. Two types of abundant mappings may be associated with synergies, descending (from a higher level to a lower level) and ascending (from a lower level to a higher level).

Fig. 2.

Top two panels are time series plots of across-subjects average force production and moment of force production. Bottom four panels are time series plots of across-subjects average force production by each finger in feedback condition separately (no feedback, solid line; force feedback, dashed line; moment feedback, dotted line), with shading indicating SE. Vertical dashed line indicates the time of feedback alteration. MVC, maximum voluntary contraction.

Fig. 3.

Average across-subjects changes in force production (ΔF) observed during each feedback condition in individual fingers (I, index; M, middle; R, ring; L, little) from the initial time point (under full visual feedback) to the end of the trial (after the feedback was differentially altered depending on the experimental condition). Error bars indicate SE. MVC, maximum voluntary contraction.

Fig. 4.

Average across-subjects magnitudes of R_SD, the ratio of the mean standard deviation of permuted data to that of nonpermuted data with respect to total force (F_TOT; top) or moment of force (M_TOT; bottom) under full feedback (open bars) or altered feedback (solid bars). Error bars indicate SE.

Fig. 5.

Values of {X_R; k}, the related pair of variables for the spatial referent coordinate and apparent stiffness, for a representative subject at the hand level (top) and individual finger level (bottom) in the no-feedback condition. Triangles represent {X_R; k} pairs recorded under full visual feedback; circles represent pairs recorded after feedback alteration. Best hyperbolic fits are represented with solid (visual feedback) or dashed (altered feedback) lines.

Fig. 6.

Across-subjects averages of change in finger-level referent coordinate (ΔX_Rf; top) and apparent stiffness (Δk_f; bottom), where f = I (index), M (middle), R (ring), and L (little). Error bars represent SE.

Fig. 7.

Across-subjects values of R_SD, the ratio of the mean standard deviation of permuted data to that of nonpermuted data, for analysis of individual finger force-stabilizing {X_Rf; k_f}, the pair of variables for the referent coordinate and apparent stiffness, during no-feedback (top), force-feedback (middle), and moment-feedback conditions (bottom). Error bars are SE.

Fig. 8.

Across-subjects average index of synergy (ΔV_Z; top), variance within the uncontrolled manifold (V_UCM; middle), and variance orthogonal to the uncontrolled manifold (V_ORT; bottom) for hand-level referent coordinate (X_RH)-stabilizing ascending synergy due to covariation of the finger-level reference coordinate (X_Rf). Open bars are data recorded under full visual feedback; solid bars are data recorded after altered visual feedback. Dashed horizontal line indicates the ΔV_Z critical value. Error bars are SE.

Fig. 9.

Across-subjects average index of synergy (ΔV_Z; top), variance within the uncontrolled manifold (V_UCM; middle), and variance orthogonal to the uncontrolled manifold (V_ORT; bottom) for hand-level apparent stiffness (k_H)-stabilizing ascending synergy due to covariation of finger-level apparent stiffness (k_f). Open bars are data recorded under full visual feedback; solid bars are data recorded after altered visual feedback. Dashed horizontal line indicates ΔV_Z critical value. Error bars are SE.

Fig. 10.

Results of 3 simulations that exemplify the effects of variability of apparent stiffness, k, on the computed metrics R_SD and R². R² refers to the best-fit hyperbola denoted by the dotted lines in A–C; R_SD is the ratio of mean standard deviation of permuted data to nonpermuted data (see methods). In each simulation, 1,000 force (F) and k values (denoted by open circles) were randomly selected from independent normal distributions. In A–C, the mean of the normal distributions from which F samples were selected = 1.0, and standard deviation = 0.1. The mean of the normal distribution for k = 1.0; in A, the standard deviation of the k distribution = 0.1; in B, the standard deviation of this distribution = 0.01; and in C, the standard deviation = 0.4. The values of mean (μ) and standard deviation (σ) in the panels refer to the sample means and standard deviations of the actual data used in the simulations.