Development, Validation, and Dissemination of a Breast Cancer Recurrence Detection and Timing Informatics Algorithm

Abstract

Background: This study developed, validated, and disseminated a generalizable informatics algorithm for detecting breast cancer recurrence and timing using a gold standard measure of recurrence coupled with data derived from a readily available common data model that pools health insurance claims and electronic health records data.

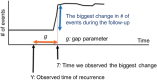
Methods: The algorithm has two parts: to detect the presence of recurrence and to estimate the timing of recurrence. The primary data source was the Cancer Research Network Virtual Data Warehouse (VDW). Sixteen potential indicators of recurrence were considered for model development. The final recurrence detection and timing models were determined, respectively, by maximizing the area under the ROC curve (AUROC) and minimizing average absolute error. Detection and timing algorithms were validated using VDW data in comparison with a gold standard recurrence capture from a third site in which recurrences were validated through chart review. Performance of this algorithm, stratified by stage at diagnosis, was compared with other published algorithms. All statistical tests were two-sided.

Results: Detection model AUROCs were 0.939 (95% confidence interval [CI] = 0.917 to 0.955) in the training data set (n = 3370) and 0.956 (95% CI = 0.944 to 0.971) and 0.900 (95% CI = 0.872 to 0.928), respectively, in the two validation data sets (n = 3370 and 3961, respectively). Timing models yielded average absolute prediction errors of 12.6% (95% CI = 10.5% to 14.5%) in the training data and 11.7% (95% CI = 9.9% to 13.5%) and 10.8% (95% CI = 9.6% to 12.2%) in the validation data sets, respectively, and were statistically significantly lower by 12.6% (95% CI = 8.8% to 16.5%, P < .001) than those estimated using previously reported timing algorithms. Similar covariates were included in both detection and timing algorithms but differed substantially from previous studies.

Conclusions: Valid and reliable detection of recurrence using data derived from electronic medical records and insurance claims is feasible. These tools will enable extensive, novel research on quality, effectiveness, and outcomes for breast cancer patients and those who develop recurrence.

Figure 1.

Phase II timing algorithm: trajectory of events and predicted time of recurrence. The chart shows an example of the trajectory of the number of events in one patient. Y on the x-axis denotes the time of the true recurrence we would like to identify. T indicates the time point where we observe the biggest change in the trajectory of the number of events during the follow-up. Note that both Y and T are observable in the gold standard data, which allows us to estimate the gap parameter “g” that indicates the difference between Y and T. Let g* be an estimate for the “g” parameter. The predicted time of recurrence, Y*, is then given by T-g*.

Figure 2.

HMO–Cancer Research Network Virtual Data Warehouse breast cancer RECUR algorithm. This figure shows components of the phase I and II breast cancer RECUR algorithm. For the phase I algorithm, there are two stages. First, we identified patients who had more than 34 secondary malignant neoplasm codes and classified these patients as having recurrence. Then, for the remaining patients, we created a logistic regression model that generated a probability of having recurrence. The figure lists each of the variables contributing to the logistic regression model with their categories, and the corresponding odds ratios with their 95% confidence intervals. The secondary malignancy codes included ICD-9 codes for 197.x–198.x, but not 196.x (lymph node metastases). For the phase I logistic regression model, the probability threshold that maximized accuracy was 34.2%, and the probability threshold that maximized the Youden index was 9.6%. The phase II algorithm estimates the timing of the recurrence event. Each variable in the timing estimation algorithm is listed with its offset (the average of the difference between the time when the component variable count peaked and the time of the gold standard recurrence) and weight (the amount a component variable’s estimated recurrence date contributed to final estimated date of recurrence). CI = confidence interval; OR = odds ratio.