Data-driven forecasting of high-dimensional chaotic systems with long short-term memory networks
- PMID: 29887750
- PMCID: PMC5990702
- DOI: 10.1098/rspa.2017.0844
Data-driven forecasting of high-dimensional chaotic systems with long short-term memory networks
Abstract
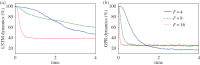
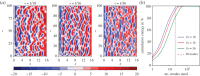
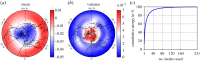
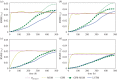
We introduce a data-driven forecasting method for high-dimensional chaotic systems using long short-term memory (LSTM) recurrent neural networks. The proposed LSTM neural networks perform inference of high-dimensional dynamical systems in their reduced order space and are shown to be an effective set of nonlinear approximators of their attractor. We demonstrate the forecasting performance of the LSTM and compare it with Gaussian processes (GPs) in time series obtained from the Lorenz 96 system, the Kuramoto-Sivashinsky equation and a prototype climate model. The LSTM networks outperform the GPs in short-term forecasting accuracy in all applications considered. A hybrid architecture, extending the LSTM with a mean stochastic model (MSM-LSTM), is proposed to ensure convergence to the invariant measure. This novel hybrid method is fully data-driven and extends the forecasting capabilities of LSTM networks.
Keywords: Gaussian processes; Lorenz 96; T21 barotropic climate model; data-driven forecasting; long short-term memory.
Conflict of interest statement
We declare we have no competing interests.
Figures
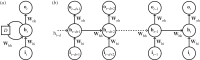
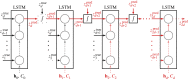

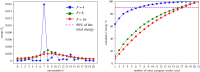

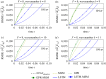

References
-
- Rowley CW. 2005. Model reduction for fluids, using balanced proper orthogonal decomposition. Int. J. Bifurcation Chaos 15, 997–1013. (doi:10.1142/S0218127405012429) - DOI
-
- Williams MO, Kevrekidis IG, Rowley CW. 2015. A data-driven approximation of the Koopman operator: extending dynamic mode decomposition. J. Nonlinear Sci. 25, 1307–1346. (doi:10.1007/s00332-015-9258-5) - DOI
-
- Tu JH, Rowley CW, Luchtenburg DM, Brunton SL, Kutz JN. 2014. On dynamic mode decomposition: theory and applications. J. Comput. Dyn. 1, 391–421. (doi:10.3934/jcd.2014.1.391) - DOI
-
- Kutz JN, Fu X, Brunton SL. 2016. Multiresolution dynamic mode decomposition. SIAM. J. Appl. Dyn. Syst. 15, 713–735. (doi:10.1137/15M1023543) - DOI
-
- Arbabi H, Mezic I. 2017. Ergodic theory, dynamic mode decomposition and computation of spectral properties of the Koopman operator. SIAM. J. Appl. Dyn. Syst. 16, 2096–2126. (doi:10.1137/17M1125236) - DOI
Associated data
LinkOut - more resources
Full Text Sources
Other Literature Sources

