Stochastic Turing patterns in a synthetic bacterial population
- PMID: 29891706
- PMCID: PMC6042114
- DOI: 10.1073/pnas.1720770115
Stochastic Turing patterns in a synthetic bacterial population
Abstract
The origin of biological morphology and form is one of the deepest problems in science, underlying our understanding of development and the functioning of living systems. In 1952, Alan Turing showed that chemical morphogenesis could arise from a linear instability of a spatially uniform state, giving rise to periodic pattern formation in reaction-diffusion systems but only those with a rapidly diffusing inhibitor and a slowly diffusing activator. These conditions are disappointingly hard to achieve in nature, and the role of Turing instabilities in biological pattern formation has been called into question. Recently, the theory was extended to include noisy activator-inhibitor birth and death processes. Surprisingly, this stochastic Turing theory predicts the existence of patterns over a wide range of parameters, in particular with no severe requirement on the ratio of activator-inhibitor diffusion coefficients. To explore whether this mechanism is viable in practice, we have genetically engineered a synthetic bacterial population in which the signaling molecules form a stochastic activator-inhibitor system. The synthetic pattern-forming gene circuit destabilizes an initially homogenous lawn of genetically engineered bacteria, producing disordered patterns with tunable features on a spatial scale much larger than that of a single cell. Spatial correlations of the experimental patterns agree quantitatively with the signature predicted by theory. These results show that Turing-type pattern-forming mechanisms, if driven by stochasticity, can potentially underlie a broad range of biological patterns. These findings provide the groundwork for a unified picture of biological morphogenesis, arising from a combination of stochastic gene expression and dynamical instabilities.
Keywords: Turing patterns; biofilm; signaling molecules; stochastic gene expression; synthetic biology.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
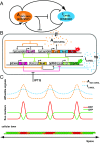
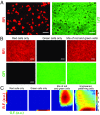
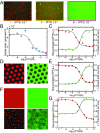

References
-
- Gierer A, Meinhardt H. A theory of biological pattern formation. Biol Cybern. 1972;12:30–39. - PubMed
-
- Castets V, Dulos E, Boissonade J, De Kepper P. Experimental evidence of a sustained standing Turing-type nonequilibrium chemical pattern. Phys Rev Lett. 1990;64:2953–2956. - PubMed
-
- Raspopovic J, Marcon L, Russo L, Sharpe J. Digit patterning is controlled by a Bmp-Sox9-Wnt Turing network modulated by morphogen gradients. Science. 2014;345:566–570. - PubMed
-
- Butler T, Goldenfeld N. Robust ecological pattern formation induced by demographic noise. Phys Rev E. 2009;80:030902. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

