Survival and weak chaos
- PMID: 29892407
- PMCID: PMC5990807
- DOI: 10.1098/rsos.172181
Survival and weak chaos
Abstract
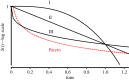
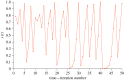
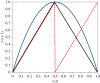
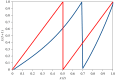
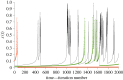
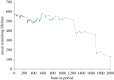
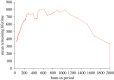
Survival analysis in biology and reliability theory in engineering concern the dynamical functioning of bio/electro/mechanical units. Here we incorporate effects of chaotic dynamics into the classical theory. Dynamical systems theory now distinguishes strong and weak chaos. Strong chaos generates Type II survivorship curves entirely as a result of the internal operation of the system, without any age-independent, external, random forces of mortality. Weak chaos exhibits (a) intermittency and (b) Type III survivorship, defined as a decreasing per capita mortality rate: engineering explicitly defines this pattern of decreasing hazard as 'infant mortality'. Weak chaos generates two phenomena from the normal functioning of the same system. First, infant mortality-sensu engineering-without any external explanatory factors, such as manufacturing defects, which is followed by increased average longevity of survivors. Second, sudden failure of units during their normal period of operation, before the onset of age-dependent mortality arising from senescence. The relevance of these phenomena encompasses, for example: no-fault-found failure of electronic devices; high rates of human early spontaneous miscarriage/abortion; runaway pacemakers; sudden cardiac death in young adults; bipolar disorder; and epilepsy.
Keywords: Pomeau–Manneville map; chaos; infant mortality; life-history theory; reliability theory; survival analysis.
Conflict of interest statement
We have no competing interests.
Figures
Similar articles
-
The connections between the frustrated chaos and the intermittency chaos in small Hopfield networks.Neural Netw. 2002 Dec;15(10):1197-204. doi: 10.1016/s0893-6080(02)00096-5. Neural Netw. 2002. PMID: 12425438
-
Singularity of Lévy walks in the lifted Pomeau-Manneville map.Chaos. 2025 Jan 1;35(1):013151. doi: 10.1063/5.0243549. Chaos. 2025. PMID: 39869920
-
Nonstationary Pomeau-Manneville intermittency in systems with a periodic parameter change.Phys Rev E Stat Nonlin Soft Matter Phys. 2006 Jun;73(6 Pt 2):066203. doi: 10.1103/PhysRevE.73.066203. Epub 2006 Jun 2. Phys Rev E Stat Nonlin Soft Matter Phys. 2006. PMID: 16906942
-
Is there chaos in the brain? II. Experimental evidence and related models.C R Biol. 2003 Sep;326(9):787-840. doi: 10.1016/j.crvi.2003.09.011. C R Biol. 2003. PMID: 14694754 Review.
-
Weak and strong chaos in Fermi-Pasta-Ulam models and beyond.Chaos. 2005 Mar;15(1):15106. doi: 10.1063/1.1849131. Chaos. 2005. PMID: 15836283 Review.
Cited by
-
Physical models of infant mortality: implications for defects in biological systems.J Biol Phys. 2020 Dec;46(4):371-394. doi: 10.1007/s10867-020-09559-0. Epub 2020 Nov 25. J Biol Phys. 2020. PMID: 33237338 Free PMC article.
-
Caputo Fractional Derivative and Quantum-Like Coherence.Entropy (Basel). 2021 Feb 9;23(2):211. doi: 10.3390/e23020211. Entropy (Basel). 2021. PMID: 33572106 Free PMC article.
References
-
- May RM. 1976. Simple mathematical models with very complicated dynamics. Nature 261, 459–467. (doi:10.1038/261459a0) - DOI - PubMed
-
- Dawkins R. 1986. The blind watchmaker: why the evidence of evolution reveals a universe without design. New York, NY: WW Norton & Company.
-
- Elsayed EA. 2012. Reliability engineering. Hoboken, NJ: John Wiley & Sons.
-
- Information Technology Laboratory. 2012. e-Handbook of statistical methods. USA: National Institute of Standards and Technology; See http://www.itl.nist.gov/div898/handbook/.
-
- Kececioglu D. 2002. Reliability engineering handbook. Lancaster, PA: DEStech Publications, Inc.
LinkOut - more resources
Full Text Sources
Other Literature Sources

