Phoretic interactions and oscillations in active suspensions of growing Escherichia coli

Abstract

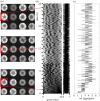
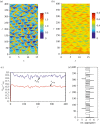
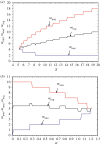
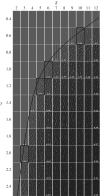
Bioluminescence imaging experiments were carried out to characterize spatio-temporal patterns of bacterial self-organization in active suspensions (cultures) of bioluminescent Escherichia coli and its mutants. An analysis of the effects of mutations shows that spatio-temporal patterns formed in standard microtitre plates are not related to the chemotaxis system of bacteria. In fact, these patterns are strongly dependent on the properties of mutants that characterize them as self-phoretic (non-flagellar) swimmers. In particular, the observed patterns are essentially dependent on the efficiency of proton translocation across membranes and the smoothness of the cell surface. These characteristics can be associated, respectively, with the surface activity and the phoretic mobility of a colloidal swimmer. An analysis of the experimental data together with mathematical modelling of pattern formation suggests the following: (1) pattern-forming processes can be described by Keller-Segel-type models of chemotaxis with logistic cell kinetics; (2) active cells can be seen as biochemical oscillators that exhibit phoretic drift and alignment; and (3) the spatio-temporal patterns in a suspension of growing E. coli form due to phoretic interactions between oscillating cells of high metabolic activity.

Keywords: Janus particles; bacterial chemotaxis; bacterial growth; biochemical oscillations; self-phoresis.

Figure 1.

Spatio-temporal patterns of bacterial luminescence. (a) Examples of images taken at different times. Images of suspensions of E. coli (first column from the left) and its mutants deficient in NhaA (second column), NhaB (third column), ChaA (fourth column) were taken 1, 12 and 23 h after plate filling. The ratio between luminescence intensities in the brightest and the darkest areas in each sample is approximately 2.5. (b) Example space–time plots (kymographs) obtained from the data of bioluminescence intensity measurements along the three-phase contact line (22 mm) and across the diameter (7 mm) of the microtitre plate well. The corresponding well is marked by the square in (a). (c) The results of the corresponding (b) data processing are represented by the number of aggregates fluctuating over time.

Figure 2.

Mutations and their influence on patterns of self-organization. (a) A scheme of bacterial cell components, which were changed by mutations. The transport of protons across outer and inner membranes of E. coli is illustrated on the same figure. In each mutant, the gene encoding an individual protein was deleted. These genes are responsible for the synthesis of proteins which are related to respiration (blue), ion channels (orange), surface appendages (red) and chemotaxis (green). (b) The average numbers of aggregates formed by E. coli DH10β and its mutants in microtitre plate wells.

Figure 3.

Simulated space–time plots of the dimensionless cell density n(x, t) (a) and the chemoattractant concentration c(x, t) (b), and the dynamics of the corresponding averaging values n_avg(t) and c_avg(t) for the contact line (c). The results of the corresponding (a) data processing are represented by the number of aggregates fluctuating over time (d). Values of other model parameters are as defined in equation (3.2).

Figure 4.

The minimal (m_min), maximal (m_max) and mean (m_avg) numbers of unstable aggregates versus the chemotactic sensitivity χ at α = 1 (a) and the cell growth rate α at χ = 6 (b). Values of the other model parameters are as defined in equation (3.2).

Figure 5.

Spatio-temporal patterns of the cell density n(x, t) simulated for different values of chemotactic sensitivity χ and the cell growth rate α. The solid lines correspond to the bifurcation conditions (precise and its linear approximation) given by equation (3.6). Values of the other model parameters are as defined in equation (3.2).

Figure 6.

Spatio-temporal patterns of the cell density simulated for different values of the production γ and degradation δ of the chemoattractant. The solid line shows the bifurcation conditions (precise and its linear approximation) given by equation (3.8). Values of the other model parameters are as defined in equation (3.2).

Figure 7.

Spatio-temporal patterns of the cell density simulated for different values of chemotactic sensitivity χ and chemoattractant production γ. The solid line shows the bifurcation condition given by equation (3.10). Values of the other model parameters are as defined in equation (3.2).

Figure 8.

A model of aerobically growing E. coli cell. A metabolically active cell is considered as a pole-to-pole oscillator that moves chemotactically (curved line) like a chemical reaction-driven Janus particle in the inhomogeneous chemical (phoretic) field, which is generated by all other colloids (blue triangle). The patterns of chemotaxis were observed when the lifetime of the phoretic field is much longer than the period of oscillations.