Individual-based modelling and control of bovine brucellosis
- PMID: 29892455
- PMCID: PMC5990817
- DOI: 10.1098/rsos.180200
Individual-based modelling and control of bovine brucellosis
Abstract
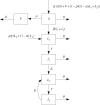
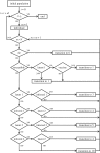
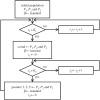
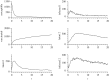
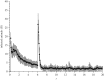
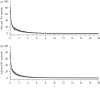
We present a theoretical approach to control bovine brucellosis. We have used individual-based modelling, which is a network-type alternative to compartmental models. Our model thus considers heterogeneous populations, and spatial aspects such as migration among herds and control actions described as pulse interventions are also easily implemented. We show that individual-based modelling reproduces the mean field behaviour of an equivalent compartmental model. Details of this process, as well as flowcharts, are provided to facilitate the reproduction of the presented results. We further investigate three numerical examples using real parameters of herds in the São Paulo state of Brazil, in scenarios which explore eradication, continuous and pulsed vaccination and meta-population effects. The obtained results are in good agreement with the expected behaviour of this disease, which ultimately showcases the effectiveness of our theory.
Keywords: bovine brucellosis; individual-based model; mathematical epidemiology.
Conflict of interest statement
The authors declare that they have no competing interests.
Figures

Similar articles
-
Large-scale study of herd-level risk factors for bovine brucellosis in Brazil.Acta Trop. 2016 Dec;164:226-232. doi: 10.1016/j.actatropica.2016.09.016. Epub 2016 Sep 21. Acta Trop. 2016. PMID: 27664333
-
Economic analysis of vaccination to control bovine brucellosis in the States of Sao Paulo and Mato Grosso, Brazil.Prev Vet Med. 2015 Mar 1;118(4):351-8. doi: 10.1016/j.prevetmed.2014.12.010. Epub 2014 Dec 22. Prev Vet Med. 2015. PMID: 25548080
-
Control of Bovine Brucellosis from Persistently Infected Holdings Using RB51 Vaccination with Test-and-Slaughter: A Comparative Case Report from a High Incidence Area in Portugal.Transbound Emerg Dis. 2016 Feb;63(1):e39-47. doi: 10.1111/tbed.12228. Epub 2014 Apr 17. Transbound Emerg Dis. 2016. PMID: 24739513
-
Bovine brucellosis control and eradication programme in Chile: vaccine use as a tool within the programme.Dev Biol (Basel). 2004;119:473-9. Dev Biol (Basel). 2004. PMID: 15742662 Review.
-
A method of accelerated eradication of bovine brucellosis in the Czech Republic.Rev Sci Tech. 2003 Dec;22(3):1003-12. doi: 10.20506/rst.22.3.1447. Rev Sci Tech. 2003. PMID: 15005556 Review.
Cited by
-
Modeling and dynamic analysis of tuberculosis in mainland China from 1998 to 2017: the effect of DOTS strategy and further control.Theor Biol Med Model. 2020 May 4;17(1):6. doi: 10.1186/s12976-020-00124-9. Theor Biol Med Model. 2020. PMID: 32362279 Free PMC article.
-
Bovine brucellosis - a comprehensive review.Vet Q. 2021 Jan 1;41(1):61-88. doi: 10.1080/01652176.2020.1868616. Vet Q. 2021. PMID: 33353489 Free PMC article. Review.
-
Application of Optimal Control of Infectious Diseases in a Model-Free Scenario.SN Comput Sci. 2021;2(5):405. doi: 10.1007/s42979-021-00794-3. Epub 2021 Aug 7. SN Comput Sci. 2021. PMID: 34396152 Free PMC article.
-
Assessing the efficiency of the bovine brucellosis surveillance-control system in a disease-free context through agent-based modelling.Vet Res. 2025 Jun 17;56(1):120. doi: 10.1186/s13567-025-01549-1. Vet Res. 2025. PMID: 40528235 Free PMC article.
References
-
- Borba MR. 2013. Prevalence and risk-mapping of bovine brucellosis in Maranhão State, Brazil. Prev. Vet. Med. 110, 169–176. (doi:10.1016/j.prevetmed.2012.11.013) - DOI - PubMed
-
- Musallam II, Abo-Shehada M, Omar M, Guitian J. 2015. Cross-sectional study of brucellosis in Jordan: prevalence, risk factors and spatial distribution in small ruminants and cattle. Prev. Vet. Med. 118, 387–396. (doi:10.1016/j.prevetmed.2014.12.020) - DOI - PubMed
-
- Souza VAF, Ferreira Neto JS, Amaku M, Dias RA, Telles EO, Hildebrand Grisi-Filho JH, Heinemann MB, Ferreira F. 2016. Mathematical modeling of bovine brucellosis control using the RB51 vaccine. Semina: Ciênc. Agrár. 37, 3767–3775. (doi:10.5433/1679-0359.2016v37n5Supl2p3767) - DOI
-
- Inchaisri C, Prasomsri P, Boonserm T, Hogeveen H, Ajariyakajorn K. 2016. A stochastic simulation model for brucellosis eradication in goat flocks in an area with high flock prevalence but low animal prevalence. Small Ruminant Res. 136, 227–237. (doi:10.1016/j.smallrumres.2016.02.005) - DOI
-
- Hou Q, Zhang F. 2016. Global dynamics of a general brucellosis model with discrete delay. J. Appl. Anal. Comput. 6, 227–241. (doi:10.11948/2016019) - DOI
LinkOut - more resources
Full Text Sources
Other Literature Sources

