Antithetic proportional-integral feedback for reduced variance and improved control performance of stochastic reaction networks

Abstract

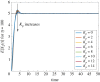
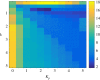
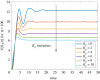
The ability of a cell to regulate and adapt its internal state in response to unpredictable environmental changes is called homeostasis and this ability is crucial for the cell's survival and proper functioning. Understanding how cells can achieve homeostasis, despite the intrinsic noise or randomness in their dynamics, is fundamentally important for both systems and synthetic biology. In this context, a significant development is the proposed antithetic integral feedback (AIF) motif, which is found in natural systems, and is known to ensure robust perfect adaptation for the mean dynamics of a given molecular species involved in a complex stochastic biomolecular reaction network. From the standpoint of applications, one drawback of this motif is that it often leads to an increased cell-to-cell heterogeneity or variance when compared to a constitutive (i.e. open-loop) control strategy. Our goal in this paper is to show that this performance deterioration can be countered by combining the AIF motif and a negative feedback strategy. Using a tailored moment closure method, we derive approximate expressions for the stationary variance for the controlled network that demonstrate that increasing the strength of the negative feedback can indeed decrease the variance, sometimes even below its constitutive level. Numerical results verify the accuracy of these results and we illustrate them by considering three biomolecular networks with two types of negative feedback strategies. Our computational analysis indicates that there is a trade-off between the speed of the settling-time of the mean trajectories and the stationary variance of the controlled species; i.e. smaller variance is associated with larger settling-time.

Keywords: antithetic integral control; cybergenetics; homeostasis; stochastic reaction networks.

Figure 1.

A reaction network controlled with an antithetic integral controller.

Figure 2.

Absolute value of the relative error between the exact stationary variance of the protein copy number and the approximate formula (2.12) when the gene expression network is controlled with the antithetic integral controller (1.2) and an ON/OFF proportional controller. (Online version in colour.)

Figure 3.

Mean trajectories for the protein copy number when the gene expression network is controlled with the antithetic integral controller (1.2) with k = 3 and an ON/OFF proportional controller. The set-point value is indicated as a black dotted line. (Online version in colour.)

Figure 4.

Variance trajectories for the protein copy number when the gene expression network is controlled with the antithetic integral controller (1.2) with k = 3 and an ON/OFF proportional controller. The stationary constitutive variance is equal to 6.1111 and is depicted in black dotted line. (Online version in colour.)

Figure 5.

Stationary variance for the protein copy number when the gene expression network is controlled with the antithetic integral controller (1.2) and an ON/OFF proportional controller. (Online version in colour.)

Figure 6.

Settling-time for the mean trajectories for the protein copy number when the gene expression network is controlled with the antithetic integral controller (1.2) and an ON/OFF proportional controller. (Online version in colour.)

Figure 7.

Absolute value of the relative error between the exact stationary variance of the protein copy number and the approximate formula (2.12) when the gene expression network is controlled with the antithetic integral controller (1.2) and a Hill controller. (Online version in colour.)

Figure 8.

Mean trajectories for the protein copy number when the gene expression network is controlled with the antithetic integral controller (1.2) with k = 3 and a Hill controller. The set-point value is indicated as a black dotted line. (Online version in colour.)

Figure 9.

Variance trajectories for the protein copy number when the gene expression network is controlled with the antithetic integral controller (1.2) with k = 3 and a Hill controller. The stationary constitutive variance is depicted in black dotted line. (Online version in colour.)

Figure 10.

Stationary variance for the protein copy number when the gene expression network is controlled with the antithetic integral controller (1.2) and a Hill controller. (Online version in colour.)

Figure 11.

Settling-time for the mean trajectories for the protein copy number when the gene expression network is controlled with the antithetic integral controller (1.2) and a Hill controller. (Online version in colour.)

Figure 12.

Mean trajectories for the mature protein copy number when the gene expression network with protein maturation is controlled with the antithetic integral controller (1.2) with k = 3 and an ON/OFF proportional controller. The set-point value is indicated as a black dotted line. (Online version in colour.)

Figure 13.

Variance trajectories for the mature protein copy number when the gene expression network with protein maturation is controlled with the antithetic integral controller (1.2) with k = 3 and an ON/OFF proportional controller. The stationary constitutive variance is depicted in black dotted line. (Online version in colour.)

Figure 14.

Settling-time for the mean trajectories for the mature protein copy number when the gene expression network with protein maturation is controlled with the antithetic integral controller (1.2) and an ON/OFF proportional controller. (Online version in colour.)

Figure 15.

Stationary variance for the mature protein copy number when the gene expression network with protein maturation is controlled with the antithetic integral controller (1.2) and an ON/OFF proportional controller. (Online version in colour.)

Figure 16.

Mean trajectories for the homodimer copy number when the gene expression network with protein dimerization is controlled with the antithetic integral controller (1.2) with k = 3 and an ON/OFF proportional controller. The set-point value is indicated as a black dotted line. (Online version in colour.)

Figure 17.

Variance trajectories for the homodimer copy number when the gene expression network with protein dimerization is controlled with the antithetic integral controller (1.2) with k = 3 and an ON/OFF proportional controller. (Online version in colour.)

Figure 18.

Stationary variance for the homodimer copy number when the gene expression network with protein dimerization is controlled with the antithetic integral controller (1.2) and an ON/OFF proportional controller. (Online version in colour.)

Figure 19.

Settling-time for the mean trajectories for the homodimer copy number when the gene expression network with protein dimerization is controlled with the antithetic integral controller (1.2) and an ON/OFF proportional controller. (Online version in colour.)