Direction-dependent interaction rules enrich pattern formation in an individual-based model of collective behavior
- PMID: 29902189
- PMCID: PMC6002104
- DOI: 10.1371/journal.pone.0198550
Direction-dependent interaction rules enrich pattern formation in an individual-based model of collective behavior
Abstract
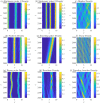
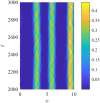
Direction-dependent interaction rules are incorporated into a one-dimensional discrete-time stochastic individual-based model (IBM) of collective behavior to compare pattern formation with an existing partial differential equation (PDE) model. The IBM is formulated in terms of three social interaction forces: repulsion, alignment, and attraction, and includes information regarding conspecifics' direction of travel. The IBM produces a variety of spatial patterns which qualitatively match patterns observed in a PDE model. The addition of direction-dependent interaction rules exemplifies how directional information transfer within a group of individuals can result in enriched pattern formation. Our individual-based modelling framework reveals the influence that direction-dependent interaction rules such as biological communication can have upon individual movement trajectories and how these trajectories combine to form group patterns.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures


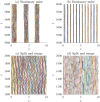
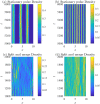
Similar articles
-
Territorial pattern formation in the absence of an attractive potential.J Math Biol. 2016 Jan;72(1-2):25-46. doi: 10.1007/s00285-015-0881-4. Epub 2015 Mar 31. J Math Biol. 2016. PMID: 25822451
-
Swarming in homogeneous environments: a social interaction based framework.J Theor Biol. 2010 Jun 7;264(3):747-59. doi: 10.1016/j.jtbi.2010.02.016. Epub 2010 Mar 6. J Theor Biol. 2010. PMID: 20211189
-
Modeling group formation and activity patterns in self-organizing collectives of individuals.Bull Math Biol. 2007 Jul;69(5):1537-65. doi: 10.1007/s11538-006-9175-8. Epub 2007 Feb 15. Bull Math Biol. 2007. PMID: 17577602
-
Examination of an averaging method for estimating repulsion and attraction interactions in moving groups.PLoS One. 2020 Dec 9;15(12):e0243631. doi: 10.1371/journal.pone.0243631. eCollection 2020. PLoS One. 2020. PMID: 33296438 Free PMC article.
-
Modelling collective cell motion: are on- and off-lattice models equivalent?Philos Trans R Soc Lond B Biol Sci. 2020 Sep 14;375(1807):20190378. doi: 10.1098/rstb.2019.0378. Epub 2020 Jul 27. Philos Trans R Soc Lond B Biol Sci. 2020. PMID: 32713300 Free PMC article. Review.
Cited by
-
Excessive Nitrogen Fertilization Favors the Colonization, Survival, and Development of Sogatella furcifera via Bottom-Up Effects.Plants (Basel). 2021 Apr 27;10(5):875. doi: 10.3390/plants10050875. Plants (Basel). 2021. PMID: 33925283 Free PMC article.
References
-
- Parrish JK. Using behavior and ecology to exploit schooling fishes. Environmental Biology of Fishes. 1999;55(1/2):157–181. doi: 10.1023/A:1007472602017 - DOI
-
- Simpson SJ, Mccaffery AR, Hägele BF. A behavioural analysis of phase change in the desert locust. Biological Reviews. 2007;74(4):461–480. doi: 10.1017/S000632319900540X - DOI
-
- Kube CR, Zhang H. Collective Robotics: From Social Insects to Robots. Adaptive Behavior. 1993;2(2):189–218. doi: 10.1177/105971239300200204 - DOI
-
- Eftimie R. Hyperbolic and kinetic models for self-organized biological aggregations and movement: a brief review. Journal of Mathematical Biology. 2012;65(1):35–75. doi: 10.1007/s00285-011-0452-2 - DOI - PubMed
-
- Miller JM, Kolpas A, Juchem Neto JP, Rossi LF. A Continuum Three-Zone Model for Swarms. Bulletin of Mathematical Biology. 2012;74(3):536–561. doi: 10.1007/s11538-011-9676-y - DOI - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

