Models for analyzing zero-inflated and overdispersed count data: an application to cigarette and marijuana use

Abstract

Introduction: This paper describes different methods for analyzing counts and illustrates their use on cigarette and marijuana smoking data.

Methods: The Poisson, zero-inflated Poisson (ZIP), hurdle Poisson (HUP), negative binomial (NB), zero-inflated negative binomial (ZINB) and hurdle negative binomial (HUNB) regression models are considered. The different approaches are evaluated in terms of the ability to take into account zero-inflation (extra zeroes) and overdispersion (variance larger than expected) in count outcomes, with emphasis placed on model fit, interpretation, and choosing an appropriate model given the nature of the data. The illustrative data example focuses on cigarette and marijuana smoking reports from a study on smoking habits among youth e-cigarette users with gender, age, and e-cigarette use included as predictors.

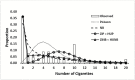
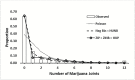
Results: Of the 69 subjects available for analysis, 36% and 64% reported smoking no cigarettes and no marijuana, respectively, suggesting both outcomes might be zero-inflated. Both outcomes were also overdispersed with large positive skew. The ZINB and HUNB models fit the cigarette counts best. According to goodness-of-fit statistics, the NB, HUNB, and ZINB models fit the marijuana data well, but the ZINB provided better interpretation.

Conclusion: In the absence of zero-inflation, the NB model fits smoking data well, which is typically overdispersed. In the presence of zero-inflation, the ZINB or HUNB model is recommended to account for additional heterogeneity. In addition to model fit and interpretability, choosing between a zero-inflated or hurdle model should ultimately depend on the assumptions regarding the zeros, study design, and the research question being asked.

Implications: Count outcomes are frequent in tobacco research and often have many zeros and exhibit large variance and skew. Analyzing such data based on methods requiring a normally distributed outcome are inappropriate and will likely produce spurious results. This study compares and contrasts appropriate methods for analyzing count data, specifically those with an over-abundance of zeros, and illustrates their use on cigarette and marijuana smoking data. Recommendations are provided.

Figure 1.

Observed versus predicted cigarette use reported on the day just before study intake. NB = negative binomial; ZIP = zero-inflated Poisson; HUP = hurdle Poisson; ZINB = zero-inflated negative binomial; HUNB = hurdle negative binomial; cigarettes use was truncated at 20 for clarity. Not shown: a single endorsement of 40 cigarettes. Note: ZIP and ZINB are modeling structural and sampling zeros.

Figure 2.

Observed versus predicted marijuana use reported on the day just before study intake. NB = negative binomial; ZIP = zero-inflated Poisson; HUP = hurdle Poisson; HUNB = hurdle negative binomial; marijuana use was truncated at 12 for clarity. Not shown: a single endorsement for 21 marijuana joints. Note: ZIP and ZINB are modeling structural and sampling zeros.