Dependence of leukocyte capture on instantaneous pulsatile flow
- PMID: 29914741
- PMCID: PMC6103190
- DOI: 10.1016/j.jbiomech.2018.05.044
Dependence of leukocyte capture on instantaneous pulsatile flow
Abstract
Atherosclerosis, an artery disease, is currently the leading cause of death in the United States in both men and women. The first step in the development of atherosclerosis involves leukocyte adhesion to the arterial endothelium. It is broadly accepted that blood flow, more specifically wall shear stress (WSS), plays an important role in leukocyte capture and subsequent development of an atherosclerotic plaque. What is less known is how instantaneous WSS, which can vary by up to 5 Pa over one cardiac cycle, influences leukocyte capture. In this paper we use direct numerical simulations (DNS), performed using an in-house code, to illustrate that leukocyte capture is different whether as a function of instantaneous or time-averaged blood flow. Specifically, a stenotic plaque is modeled using a computational fluid dynamics (CFD) solver through fully three-dimensional Navier-Stokes equations and the immersed boundary method. Pulsatile triphasic inflow is used to simulate the cardiac cycle. The CFD is coupled with an agent-based leukocyte capture model to assess the impact of instantaneous hemodynamics on stenosis growth. The computed wall shear stress agrees well with the results obtained with a commercial software, as well as with theoretical results in the healthy region of the artery. The analysis emphasizes the importance of the instantaneous flow conditions in evaluating the leukocyte rate of capture. That is, the capture rate computed from mean flow field is generally underpredicted compared to the actual rate of capture. Thus, in order to obtain a reliable estimate, the flow unsteadiness during a cardiac cycle should be taken into account.
Keywords: Direct numerical simulation; Hemodynamics; Instantaneous flow; Leukocyte capture; Time-averaged flow.
Copyright © 2018 Elsevier Ltd. All rights reserved.
Conflict of interest statement
Conflict of interest statement
The authors declare no conflict of interest.
Figures
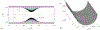
 h = 0.1D,
h = 0.1D,  h = 0.2D,
h = 0.2D,  h = 0.3D. (b) Visualization of the three-dimensional stenosis in the case h = 0.2D. Only half of the circular wall is shown. The other half is smooth.
h = 0.3D. (b) Visualization of the three-dimensional stenosis in the case h = 0.2D. Only half of the circular wall is shown. The other half is smooth.
 instantaneous bulk velocity;
instantaneous bulk velocity;  mean bulk velocity. (b) Mean flow field averaged over a cardiac cycle. (c)–(f) Instantaneous flow fields: (c) t/T = 6/32
mean bulk velocity. (b) Mean flow field averaged over a cardiac cycle. (c)–(f) Instantaneous flow fields: (c) t/T = 6/32  , (d) t/T = 14/32
, (d) t/T = 14/32  , (e) t/T = 18/32
, (e) t/T = 18/32  , (f) t/T = 30/32
, (f) t/T = 30/32  . The scales of the axes in the figures are different to show the details of the flow past the stenosis.
. The scales of the axes in the figures are different to show the details of the flow past the stenosis.

 DNS,
DNS,  theoretical value for a circular pipe, according to eq. (13); (b) instantaneous wall shear stress:
theoretical value for a circular pipe, according to eq. (13); (b) instantaneous wall shear stress:  t/T = 6/32,
t/T = 6/32,  t/T = 14/32,
t/T = 14/32, t/T = 18/32,
t/T = 18/32,  t/T = 30/32;
t/T = 30/32;  time-averaged
time-averaged
 ; value of
WSS
above which leukocytes cannot adhere,
WSS = 1.2 Pa. (c) root mean square value of WSS normalized by the healthy value WSS0.
; value of
WSS
above which leukocytes cannot adhere,
WSS = 1.2 Pa. (c) root mean square value of WSS normalized by the healthy value WSS0.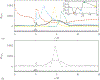
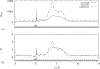
 t/T = 6/32,
t/T = 6/32,  t/T = 14/32,
t/T = 14/32,  t/T = 18/32,
t/T = 18/32,  t/T = 30/32;
t/T = 30/32;  time-averaged . (b) Comparison between using rate of capture from the mean shear, , (
time-averaged . (b) Comparison between using rate of capture from the mean shear, , ( ) and the actual mean rate of capture, , (
) and the actual mean rate of capture, , ( ).
).
 neutrophil,
neutrophil,  monocyte,
monocyte,  lymphocyte. (a) per unit concentration ρi (where i indicates the type of leukocytes); (b) actual capture rate.
lymphocyte. (a) per unit concentration ρi (where i indicates the type of leukocytes); (b) actual capture rate.
 mean rate from instantaneous shear stress ; capture rate using time-averaged wall shear stress
mean rate from instantaneous shear stress ; capture rate using time-averaged wall shear stress
 . (a) h = 0.1D; (b) h = 0.2D (same as figure 5b); (c) h = 0.3D, the scale in the inset is changed to emphasize the details of the mean capture rate distributions, .
. (a) h = 0.1D; (b) h = 0.2D (same as figure 5b); (c) h = 0.3D, the scale in the inset is changed to emphasize the details of the mean capture rate distributions, .

 straight pipe (no stenosis);
straight pipe (no stenosis); h/D = 0.1;
h/D = 0.1;  h/D = 0.2;
h/D = 0.2;  h/D = 0.3.
h/D = 0.3.Similar articles
-
Coronary artery plaque growth: A two-way coupled shear stress-driven model.Int J Numer Method Biomed Eng. 2020 Jan;36(1):e3293. doi: 10.1002/cnm.3293. Epub 2019 Dec 9. Int J Numer Method Biomed Eng. 2020. PMID: 31820589
-
Haemodynamic assessment of human coronary arteries is affected by degree of freedom of artery movement.Comput Methods Biomech Biomed Engin. 2017 Feb;20(3):260-272. doi: 10.1080/10255842.2016.1215439. Epub 2016 Jul 28. Comput Methods Biomech Biomed Engin. 2017. PMID: 27467730
-
The values of wall shear stress, turbulence kinetic energy and blood pressure gradient are associated with atherosclerotic plaque erosion in rabbits.J Atheroscler Thromb. 2014;21(8):831-8. doi: 10.5551/jat.23093. Epub 2014 Mar 25. J Atheroscler Thromb. 2014. PMID: 24671111
-
The influence of anesthesia and fluid-structure interaction on simulated shear stress patterns in the carotid bifurcation of mice.J Biomech. 2016 Sep 6;49(13):2741-2747. doi: 10.1016/j.jbiomech.2016.06.010. Epub 2016 Jun 15. J Biomech. 2016. PMID: 27342001
-
Numerical modeling of pulsatile turbulent flow in stenotic vessels.J Biomech Eng. 2003 Aug;125(4):445-60. doi: 10.1115/1.1589774. J Biomech Eng. 2003. PMID: 12968569 Review.
Cited by
-
Assessment with clinical data of a coupled bio-hemodynamics numerical model to predict leukocyte adhesion in coronary arteries.Sci Rep. 2021 Jun 16;11(1):12680. doi: 10.1038/s41598-021-92084-4. Sci Rep. 2021. PMID: 34135399 Free PMC article.
-
Bridging hemodynamics, tissue mechanics, and pathophysiology in coronary artery disease: A new agent-based model with tetrahedral mesh integration.J Biomech. 2025 Apr;183:112631. doi: 10.1016/j.jbiomech.2025.112631. Epub 2025 Mar 11. J Biomech. 2025. PMID: 40132244 Free PMC article.
References
-
- Armaly BF, Durst F, Pereira JCF, Schönung B, 1983. Experimental and theoretical investigation of backward-facing step flow. J. Fluid Mech 127, 473–496.
-
- Barreiro O, Yanez-Mo M, Sala-Valdes M, Gutierrez-Lopez MD, Ovalle S, Higginbottom A, Monk PN, Cabanas C, Sanchez-Madrid F, 2005. Endothelial tetraspanin microdomains regulate leukocyte firm adhesion during extravasation. Blood 105(7), 2852–2861. 10.1182/blood-2004-09-3606. PubMed PMID: . - DOI - PubMed
-
- Beratlis N, Balaras E, Parvinian B, Kiger K, 2005. A Numerical and Experimental Investigation of Transitional Pulsatile Flow in a Stenosed Channel. J. Biomech. Eng 127, 1147–1157. - PubMed
-
- Beratlis N, Balaras E, Kiger K, 2007. Direct numerical simulations of transitional pulsatile flow through a constriction. J. Fluid Mech. 587, 425–451.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials
Miscellaneous

