A new approach to the intracardiac inverse problem using Laplacian distance kernel

Abstract

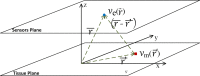
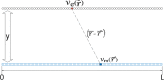
Background: The inverse problem in electrophysiology consists of the accurate estimation of the intracardiac electrical sources from a reduced set of electrodes at short distances and from outside the heart. This estimation can provide an image with relevant knowledge on arrhythmia mechanisms for the clinical practice. Methods based on truncated singular value decomposition (TSVD) and regularized least squares require a matrix inversion, which limits their resolution due to the unavoidable low-pass filter effect of the Tikhonov regularization techniques.

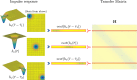
Methods: We propose to use, for the first time, a Mercer's kernel given by the Laplacian of the distance in the quasielectrostatic field equations, hence providing a Support Vector Regression (SVR) formulation by following the principles of the Dual Signal Model (DSM) principles for creating kernel algorithms.

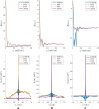
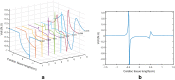
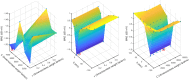
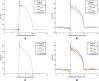
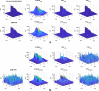
Results: Simulations in one- and two-dimensional models show the performance of our Laplacian distance kernel technique versus several conventional methods. Firstly, the one-dimensional model is adjusted for yielding recorded electrograms, similar to the ones that are usually observed in electrophysiological studies, and suitable strategy is designed for the free-parameter search. Secondly, simulations both in one- and two-dimensional models show larger noise sensitivity in the estimated transfer matrix than in the observation measurements, and DSM-SVR is shown to be more robust to noisy transfer matrix than TSVD.

Conclusion: These results suggest that our proposed DSM-SVR with Laplacian distance kernel can be an efficient alternative to improve the resolution in current and emerging intracardiac imaging systems.

Keywords: Dual Signal Model; Electrophysiology; Inverse problem; Laplacian; Mercer’s kernel; Support Vector Regression.

Fig. 1

Section of two-dimensional cardiac tissue model. The upper plane corresponds to the region where the catheters are catching the measurements, whereas the lower plane corresponds to the cardiac tissue acting as bioelectric sources

Fig. 2

Construction scheme of transfer matrix, by using a two-dimensional uniform impulse response $h_e(\overline{r})$. Note that $vect(h_e(\overline{r}-\overline{\tau }))$ denotes a vectorization of a two-dimensional impulse response shifted from the origin by $\overline{\tau }$, where ${\overline{\tau }}_1$ and ${\overline{\tau }}_2$ are two possibly different shift factors

Fig. 3

Scheme of the one-dimensional cardiac tissue model of source and catchment elements

Fig. 4

Ill-conditioning of the inverse problem in electrophysiology. A delta function is used as a source, and it is estimated in space (down) by different methods and for different SNR. The corresponding frequency responses are calculated (up): a SNR=15 dB; b SNR=25dB; c SNR=35 dB. Note that $H_{\lambda }(\omega )$ denotes the frequency response after tuning the free parameters on each method, and $h_{\lambda }(x)$ denotes the impulse response of each method

Fig. 5

Unipolar EGM waveforms obtained with different values of $z_0$, normalized to its maximum amplitude for visualization purposes (a), and with $z_0=0.02$ cm (b) on the one-dimensional tissue model

Fig. 6

Examples of free-parameter search for DSM−SVR. Blue points indicate the set of free-parameter values that were scrutinized in the search grid. Red circles indicate the obtained optimum combination for these values, to be used in the final solution

Fig. 7

Results on noise robustness of the methods in the one-dimensional model. MAE has been calculated for all the tested methods as a function of SNR (a, b) and of HNR (c, d). We also compared the classically used L-Curve (a, c) versus the LOO (b, d) as validation criterion to tune the free parameters

Fig. 8

Estimated potentials in the one-dimensional source, for all the tested methods, when tuning the free parameters in the classical algorithms with L-Curve (a, b) and with LOO (c, d), without noise (a, c) and with HNR = 45 dB (b, d)

Fig. 9

Details on the simulation results in the two-dimensional model, for SNR = 40 db. a Transmembrane potentials as a function of spatial coordinates, for the ideal and the estimated versions. b Absolute residuals for the estimated transmembrane potentials in a

Fig. 10

Details on the simulation results in the two-dimensional model, for HNR = 40 db. a Transmembrane potentials as a function of spatial coordinates, for the ideal and the estimated versions. b Absolute residuals for the estimated transmembrane potentials in (a)