Indel-correcting DNA barcodes for high-throughput sequencing

Abstract

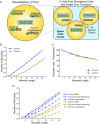
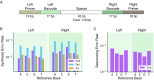
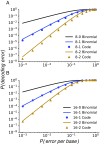
Many large-scale, high-throughput experiments use DNA barcodes, short DNA sequences prepended to DNA libraries, for identification of individuals in pooled biomolecule populations. However, DNA synthesis and sequencing errors confound the correct interpretation of observed barcodes and can lead to significant data loss or spurious results. Widely used error-correcting codes borrowed from computer science (e.g., Hamming, Levenshtein codes) do not properly account for insertions and deletions (indels) in DNA barcodes, even though deletions are the most common type of synthesis error. Here, we present and experimentally validate filled/truncated right end edit (FREE) barcodes, which correct substitution, insertion, and deletion errors, even when these errors alter the barcode length. FREE barcodes are designed with experimental considerations in mind, including balanced guanine-cytosine (GC) content, minimal homopolymer runs, and reduced internal hairpin propensity. We generate and include lists of barcodes with different lengths and error correction levels that may be useful in diverse high-throughput applications, including >10⁶ single-error-correcting 16-mers that strike a balance between decoding accuracy, barcode length, and library size. Moreover, concatenating two or more FREE codes into a single barcode increases the available barcode space combinatorially, generating lists with >10¹⁵ error-correcting barcodes. The included software for creating barcode libraries and decoding sequenced barcodes is efficient and designed to be user-friendly for the general biology community.

Keywords: DNA barcodes; error-correcting codes; information storage; massively parallel synthesis.

Fig. 1.

Applications and error correction strategies of DNA barcodes. (A) Illustrative examples of high-throughput sequencing assays that require large lists of error-correcting DNA barcodes. Barcodes are used to identify individual cells or molecules in pooled libraries (1, 10, 13). (B) Current strategies to correct synthesis and sequencing errors in DNA barcodes are confounded by indels. Hamming distance can only handle substitutions. Levenshtein distance is confounded by the fact that barcodes are prepended to other sequences of interest. Indels thus produce phantom Levenshtein distance errors when bases from the remaining DNA molecule shift into or out of the barcode window. (C) Examples of FREE divergence (this work), given the actual edit history. Levenshtein (Lev) and Hamming distances are also shown for comparison. A substitution and insertion are correctly attributed as two edits by FREE divergence (first column). FREE divergence is a symmetrical function [i.e., FreeDiv(E, O) = FreeDiv(O, E)] (first and second columns). Different actual edit paths can result in the same observed sequence (second and third columns). Indels can have zero cost, particularly near the end of the barcode, where they can occasionally be undone by fill or truncation (fourth column). Edits past the barcode end can matter since the fill/truncation step happens only upon observation (fifth column). del., deletion; div., divergence; ins., insertion; sub., substitution; trunc., truncation.

Fig. 2.

FREE barcode generation and decoding. (A) Error-correcting barcode generation is a sphere-packing problem. Around each accepted barcode B (e.g., “CTCA”), we reserve DecodeSphere_m(B), the set of all sequences within FREE divergence m of B; that is, the set of all sequences with any combination of up to m errors from B, followed by fill or truncation as necessary. (Right) Any set of disjoint decode spheres is a valid FREE code. (B) Number of single- and double-error correction barcodes generated for a range of barcode lengths. (C) Accompanying software decodes more than 120,000 barcodes per second for all barcode lengths considered here. (D) Comparison of FREE barcode counts against pruned Hamming codes and Levenshtein codes. Hamming codes were pruned to remove members that did not decode FREE divergence errors, while Levenshtein codes were produced at double the error correction levels for the same purpose. FREE codes produce more barcodes than either of the other methods for all barcode lengths.

Fig. 3.

Experimental measurement of synthesis and sequencing error rates. (A) Schematic of the DNA constructs used for barcode validation experiments. Each member in the synthetic library had a unique pair of left and right barcodes (green) drawn from a list of >8,000 17-nt FREE codes with double-error correction. By using the primer regions (brown) to distinguish the left and right ends from one another, we could determine whether the barcodes were correctly decoded (matching) or incorrectly decoded (mismatching). (B) Synthesis error rates measured in this experiment, by intended reference base and error type: substitution (Sub), deletion (Del), and insertion (Ins). (C) Measured sequencing substitution error rates by reference base. Indels from Illumina sequencing are extremely rare and are omitted for clarity.

Fig. 4.

Decoding corrupted barcodes from simulated errors. Modeled and simulated decoding error rates given the per-base error rate for length 8 (A) and length 16 (B) barcodes. Barcode sets are labeled according to length and number of errors corrected; for example, the 16-2 code is length 16 and corrects up to two errors. Solid lines show the error rate approximations using a binomial model. Circles and triangles show direct simulation error rates for single- and double-error–correcting codes, respectively. Substitution, insertion, and deletion errors each have a simulated error rate P(error per base)/3 for simplicity.

Fig. 5.

Decoding corrupted barcodes from experimental data. Observed decoding error rates compared with theoretical rates from the synthesis and sequencing error rates.

Fig. 6.

Combinatorial barcode libraries via concatenation of FREE barcodes. (A) Concatenated barcodes can be decoded sequentially in a left-to-right order, even when the end position of each edited subbarcode is not initially known. The decoded first FREE subbarcode can be used to find the starting position of the next subbarcode, and similarly for subsequent subbarcodes. (B) Concatenated barcode decoding error rates. Concatenated barcode labels use the following format: a 3 × (16-1) barcode consists of three concatenated subbarcodes, each of which is 16 bp long and can correct up to one error. Lines indicate a binomial model. Points indicate direct simulation. (C and D) Concatenating multiple barcodes combinatorially increases the numbers of effective FREE barcodes. Concatenated barcodes can correct the same number of errors per subbarcode. When the errors are distributed evenly among the subbarcodes, concatenated barcodes can correct a higher total number of errors than the individual subbarcodes. (C) Concatenated single-error–correcting barcodes. (D) Concatenated double-error–correcting barcodes. Dashed lines indicate projected quantities calculated by sampling. Dotted lines indicate log-linear projections.