Unraveling the dose-response puzzle of L. monocytogenes: A mechanistic approach

Abstract

Food-borne disease outbreaks caused by Listeria monocytogenes continue to impose heavy burdens on public health in North America and globally. To explore the threat L. monocytogenes presents to the elderly, pregnant woman and immuno-compromised individuals, many studies have focused on in-host infection mechanisms and risk evaluation in terms of dose-response outcomes. However, the connection of these two foci has received little attention, leaving risk prediction with an insufficient mechanistic basis. Consequently, there is a critical need to quantifiably link in-host infection pathways with the dose-response paradigm. To better understand these relationships, we propose a new mathematical model to describe the gastro-intestinal pathway of L. monocytogenes within the host. The model dynamics are shown to be sensitive to inoculation doses and exhibit bi-stability phenomena. Applying the model to guinea pigs, we show how it provides useful tools to identify key parameters and to inform critical values of these parameters that are pivotal in risk evaluation. Our preliminary analysis shows that the effect of gastro-environmental stress, the role of commensal microbiota and immune cells are critical for successful infection of L. monocytogenes and for dictating the shape of the dose-response curves.

Keywords: Bi-stable; Dose-response; Guinea pig; L. monocytogenes; Mechanistic model.

Fig. 1

(a) Effect of β on the existence of the threshold, L_*; (b) the density of L. monocytogenes approaches one of the two stable steady states (bi-stable phenomenon).

Fig. 2

Data fit. The squares are the numbers of L. monocytogenes in the small intestine of guinea pig (Lecuit, 2001) and the solid curve is the model prediction.

Fig. 3

Effect of β on bacteria survival: Initial dose = 1 × 10¹⁰ CFU, α = 0.18, r = 0.23, K = 3 × 10⁶, δ = 6.73.

Fig. 4

Temporal sensitivity of the model prediction L_I relative to each parameter with fixed initial dose of 1 × 10⁶ CFU. Time t_GI is indicated by the vertical dotted line. Initially, the two model parameters, δ and r, are the most sensitive whereas K becomes more sensitive at the end of simulation. This sensitivity result is reasonable as δ and r play important roles in the survival and growth of L. monocytogenes at the beginning of infection while K dominates the population when it becomes large.

Fig. 5

Dose dependent sensitivity of the model prediction L_I (at steady state) relative to each parameter. The PRCCs vary with initial doses of L. monocytogenes.

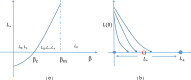
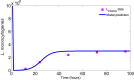
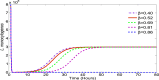
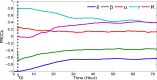
1. 1)

   According to Fig. 4, δ is the most sensitive parameter at the beginning of the infection and it remains among the top sensitive parameters during the infection. It is even more sensitive at a lower initial dose (e.g. 10⁶ CFU) (see Fig. 5). Recall that δ is the killing rate of bacteria in the stomach caused by the stomach acid. Being large, δ can reduce the initial dose of ingested bacteria below the threshold before they move down to the small intestine. Thus, large δ can effectively block the bacterial dissemination into the small intestine and across the body. Small δ, on the other hand, may allow sufficient amount of bacteria passing to the small intestine where the bacteria may colonize if not killed by the immune cells and commensals. Since δ acts on the bacteria during the first few hours of infection, the sensitivity declines quickly there after.

2. 2)

   The growth rate r plays an important role in the survival of the L. monocytogenes. Its magnitude clearly influences the population size initially, but the sensitivity of r decreases over the time as the population approaches the steady state and stabilizes (see Fig. 4). Furthermore, if r is sufficiently large then the L. monocytogenes population can survive for a longer period of time. On the other hand, with a small growth rate, L. monocytogenes may not survive against host defenses.

3. 3)

   The survival of L. monocytogenes is sensitive to the carrying capacity K in connection with the maximum level of the population and increases with the progression of time (Fig. 4). Since the carrying capacity has little effect on the initial growth or the survival of L. monocytogenes at the early stage of infection, it is not influential at the beginning of the infection. However, if the bacteria survives for a long time and continues to grow then K dominates the population, playing a more significant role. Fig. 5 also indicates that K is more sensitive at a higher inoculation dose. This is reasonable since the population more quickly reaches the carrying capacity with a higher initial dose.

4. 4)

   The killing rate, β, of L. monocytogenes in the intestine is sensitive, with negative PRCC, similar to δ and r in magnitude. The population that survives in the stomach and reaches the small intestine is killed by the host's immune cells at the rate of β. Thus β, relative to our modeling context, corresponds to the final defense posed by the host. A weak defense (immune) system, with a small β, could allow the bacteria to grow. But, a strong immune system can clear the bacteria from the small intestine before they colonize. In terms of Fig. 5, we see that for lower doses β plays a more significant role as the immune system has a higher chance of suppressing the bacterial population.

5. 5)

   The saturating constant, α, is the least sensitive among the model parameters. In the absence of α (i.e. α = 0) the bacteria may die out due to the host defense, but a positive value of α could help the bacteria survive. Note that in Fig. 5, the PRCC value of α seems to have maximum for initial doses near 10⁸ CFU. While this result is not completely clear, due to the relative low sensitivity of α we defer an in depth analysis.

Fig. 6

Effect of initial doses on the survival of L. monocytogenes. The values of the parameters are β = 0.58, α = 0.18, r = 0.23, K = 3 × 10⁶, δ = 6.73.

Fig. 7

Probability of infection with respect to various inoculum levels of L. monocytogenes.

Fig. 8

Dose-response curves with uniform distributions of r (a), and K (b). The solid curves are generated from the log-logistic model and the circles are the model generated data. The other parameters are set to the base values given in Table 1.

Fig. 9

Effect of δ on the dose-response curve. The solid curve represents the probability of infection when δ is distributed uniformly and the circles are the model generated data. The other parameters are set to the baseline values given in Table 1.

Fig. 10

The dose-response curve with a uniform distribution of β. The solid curve is generated from the log-logistic model and the circles are the model generated data. The other parameters are set to the baseline values given in Table 1.

Fig. 11

Model generated dose-response region together with an experimental result. The shaded region is the model predicted outcomes given by the distribution of β and the solid curve results from fitting a log-logistic model to the guinea pig data (Van Stelten et al., 2011). The other parameters of the model are set to the base values given in Table 1.

Fig. 12

Model generated dose-response region together with an experimental result. The shaded region is the model predicted outcomes given by the distribution of β and the solid curve results from fitting an exponential model (Haas et al., 1999) to the guinea pig data (Van Stelten et al., 2011). The other parameters of the model are set to the base values given in Table 1.