Model selection for seasonal influenza forecasting

Abstract

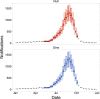
Epidemics of seasonal influenza inflict a huge burden in temperate climes such as Melbourne (Australia) where there is also significant variability in their timing and magnitude. Particle filters combined with mechanistic transmission models for the spread of influenza have emerged as a popular method for forecasting the progression of these epidemics. Despite extensive research it is still unclear what the optimal models are for forecasting influenza, and how one even measures forecast performance. In this paper, we present a likelihood-based method, akin to Bayes factors, for model selection when the aim is to select for predictive skill. Here, "predictive skill" is measured by the probability of the data after the forecasting date, conditional on the data from before the forecasting date. Using this method we choose an optimal model of influenza transmission to forecast the number of laboratory-confirmed cases of influenza in Melbourne in each of the 2010-15 epidemics. The basic transmission model considered has the susceptible-exposed-infectious-recovered structure with extensions allowing for the effects of absolute humidity and inhomogeneous mixing in the population. While neither of the extensions provides a significant improvement in fit to the data they do differ in terms of their predictive skill. Both measurements of absolute humidity and a sinusoidal approximation of those measurements are observed to increase the predictive skill of the forecasts, while allowing for inhomogeneous mixing reduces the skill. We discuss how our work could be integrated into a forecasting system and how the model selection method could be used to evaluate forecasts when comparing to multiple surveillance systems providing disparate views of influenza activity.

Fig. 1

(Top) Time series of the number of laboratory confirmed cases of influenza in Melbourne for 2010–15 aggregated by week. (Bottom) Scaled time series of the measurements of absolute humidity in Melbourne for 2010–15 in grey, with cubic spline smoothing in green and a sinusoidal approximation in blue. The minimum and maximum values over the whole six years were set to $-1$ and $1$ respectively.

Fig. 2

Graphical representation of the hidden Markov model in which the hidden state, $X_t$, represents the state of the SEIR transmission model at time t and the observations, $Y_t$, the number of notifications over the week prior. The absolute humidity signal, ${\text{AH}}_t$, is assumed to be a deterministic function of time. The arrows indicate that: the evolution of the hidden state is dependent on its current state and the AH signal, and the observations are dependent on the current state of the hidden state and its state at the previous measurement.

Fig. 3

Simulation periods for 2015. The first portion of the data (circles) is used to estimate the background notification rate via the exponentially weighted moving average (solid line). The second portion of the data is the target of the filtering and forecasting. The solid circles indicate the dates at which a forecast was generated.

Fig. 4

The $50\text{\%}$ and $95\text{\%}$ credible interval for the observations under the filtering distribution for the null and sinusoidally forced models for the 2015 notification data. These running summaries of the observation distribution demonstrate both the null and sinusoidally forced models have near identical ability to assimilate new data, i.e., they have equal now-casting capabilities.

Fig. 5

The logarithm of the aggregate Bayes factor (across all the epidemics 2010–15) for each of the alternative transmission models. The solid horizontal line indicates parity with the null model, anything above this line is an improvement in model fit over the null, and below the fit is weaker. The dashed horizontal lines indicate the significance threshold.

Fig. 6

Comparison of the forecasts from the null and sinusoidally forced transmission models using increasing amounts of data from the 2015 epidemic. The solid points represent “observed” data used to fit the model and the hollow points represent the “future” data, the target of the forecast. The logarithms of the Bayes factors reported describe the improvement in forecast performance by the sinusoidally forced model over the null for each of the forecasts generated.

Fig. 7

The logarithm of the aggregate forecast Bayes factor (across all the epidemics 2010–15) for each of the alternative transmission models. The solid horizontal line indicates parity with the null model, anything above this line is an improvement in predictive skill. The dashed horizontal lines indicate the significance threshold.

Fig. 8

Forecast error plotted against the size of the observation being forecast. Each point represents the error in attempts to forecast a single observation (averaged over the forecasts made at different points in the season). A point at $\left(x,y\right)$ indicates that when forecasting an observation of x cases the average error in the prediction was y, so negative and positive values of y indicate underestimation and overestimation respectively. The colour of each point indicates which model was used to generate the forecast. The solid lines represents a LOESS smoothing of the data.