Deciphering microbial interactions in synthetic human gut microbiome communities

Abstract

The ecological forces that govern the assembly and stability of the human gut microbiota remain unresolved. We developed a generalizable model-guided framework to predict higher-dimensional consortia from time-resolved measurements of lower-order assemblages. This method was employed to decipher microbial interactions in a diverse human gut microbiome synthetic community. We show that pairwise interactions are major drivers of multi-species community dynamics, as opposed to higher-order interactions. The inferred ecological network exhibits a high proportion of negative and frequent positive interactions. Ecological drivers and responsive recipient species were discovered in the network. Our model demonstrated that a prevalent positive and negative interaction topology enables robust coexistence by implementing a negative feedback loop that balances disparities in monospecies fitness levels. We show that negative interactions could generate history-dependent responses of initial species proportions that frequently do not originate from bistability. Measurements of extracellular metabolites illuminated the metabolic capabilities of monospecies and potential molecular basis of microbial interactions. In sum, these methods defined the ecological roles of major human-associated intestinal species and illuminated design principles of microbial communities.

Keywords: ecology; human gut microbiome; mathematical modeling; microbial community; microbial interaction.

Figure 1. Experimental design for high‐throughput characterization of synthetic human gut microbiome consortia

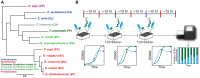
1. Phylogenetic tree of the 12‐member synthetic ecology spanning the major phyla in the gut microbiome including Actinobacteria, Bacteroidetes, Firmicutes, and Proteobacteria. Phylogenetic analysis was performed using a concatenated alignment of single‐copy marker genes obtained via PhyloSift (preprint: Darling et al, 2014). Maximum likelihood trees were generated using default options. The scale bar represents the number of substitutions per site in the alignment.

2. Schematic of the experimental design for this study. Species were combined using an approximately 1:1 or 19:1 initial proportion based on absorbance measurements at 600 nm (OD600) into microtiter plates using liquid‐handling robotic manipulation. Approximately every 12 h, samples were collected for multiplexed 16S rRNA gene sequencing (black circles). Relative abundance was measured using multiplexed 16S rRNA gene sequencing of the V3–V4 region using dual‐indexed primers compatible with an Illumina platform (stacked bar plot, bottom right). Serial transfers were performed in approximately 24 intervals (purple bars, top) by transferring an aliquot of the communities into fresh media using a 1:20 dilution. In parallel, time‐resolved OD600 measurements of monospecies and consortia were performed.

Figure 2. Model training of generalized Lotka–Volterra (gLV) to time‐resolved measurements of monospecies and pairwise assemblages

1. Species relative abundance as a function of time for all pairwise communities. Experimental measurements and model fits based on T3 are represented as data points and lines, respectively. In each subplot, time and species relative abundance are displayed on the x‐ and y‐axis, respectively. Stars denote datasets with a sum of mean squared errors greater than 0.15. Error bars represent 1 s.d. from the mean of at least three biological replicates.

2. Temporal changes in species relative abundance of a selected set of pairwise assemblages inoculated at 5% species A, 95% species B or 95% species A, 5% species B based on OD600 values. Time and relative abundance are represented on the x‐ and y‐axis, respectively. Data points and lines represent experimental measurements and model fits to T3, respectively. Error bars represent 1 s.d. from the mean of at least three biological replicates. Stars denote datasets with a sum of mean squared errors greater than 0.15.

3. Inferred inter‐species interaction coefficients for the gLV model trained on T3. Gray and green edges denote negative (α _ij < 0) and positive (α _ij > 0) interaction coefficients. The edge width and node size represent the magnitude of the inter‐species interaction coefficient and steady state monospecies abundance (x _e = −μ _i α _ii ⁻¹), respectively. To highlight significant interactions, inter‐species interaction coefficients with a magnitude less than 1e‐5 were not displayed.

Figure 3. Validation of the parameterized Lotka–Volterra model to time‐series data of informative multi‐species communities

1. Stacked bar plots of all 11 and 12‐member (full) multi‐species communities. The text above each subplot denotes the absent organism in the community. Time and relative abundance are represented on the x‐ and y‐axis of each subplot, respectively. Colors represent different organisms in the community.

2. Difference in community assembly for single‐species dropout communities. Difference in community assembly was computed as ${\sum }_{i=1}^{11},\frac{1}{7}{\sum }_{j=1}^7{\left({\widehat{v}}_{ji,\mathrm{FULL}}-v_{ji,X}\right)}^2$ where i and j represent species and time points, respectively. X represents a single‐species dropout community lacking the organism X. $\widehat{v}$ denotes the renormalized relative abundance of the shared set of species in the full (12‐member) and single‐species dropout community. Here, ${\widehat{v}}_i=\frac{v_i}{{\sum }_{i\in C}{v}_i}$ where C denotes the set of 11 shared organisms in the full and single‐species dropout community. Data points represent biological replicates (n = 6, circles) and the mean of biological replicates (blue squares), respectively.

3. Box plot of the Pearson correlation coefficient for three model training sets (left) including T1: monospecies (M); T2: M and pairwise 1 (PW1); and T3: M, PW1 and pairwise 2 (PW2). On each box, the red line represents the median, the edges of the box are the 25^th and 75^th percentiles, the whiskers extend to the most extreme data points, and the outliers are plotted as red crosses.

4. Box plot of the sum of mean squared errors for the model predictions of the time‐resolved measurements of multi‐species communities trained on T1, T2, or T3 training sets. On each box, the red line represents the median, the edges of the box are the 25^th and 75^th percentiles, the whiskers extend to the most extreme data points, and the outliers are plotted as red crosses.

5. Comparison between model predictions that trained on T1–T4 and experimental data for each organism in the full community as a function of time. On each subplot, the x‐ and y‐axis represent time and relative abundance of each species, respectively. Data points (red) and lines denote experimental data and model predictions based on T1–T4. Species names are displayed in the upper left corner of each subplot. Error bars represent 1 s.d. from the mean of six biological replicates.

Figure 4. History dependence and robust species coexistence in pairwise consortia motifs

1. History dependence due to slow relaxation to equilibrium can be augmented by negative inter‐species interactions. Model analyses of six pairwise communities that experimentally displayed history‐dependent behaviors (Appendix Fig S5B) and are coupled by mutual inhibitory interactions in the gLV model trained on T3. Network topology (left) and heat‐map of history‐dependent responses (right) across a range of inter‐species interaction coefficient values. The line width and node size of the network diagrams represent the magnitude of the inter‐species interaction coefficients and steady state monospecies abundance, respectively. The heat‐map shows the absolute value of the difference in species absolute abundance at 72 h for communities simulated using two initial conditions: x ₁ = 0.0158, x ₂ = 0.0008 or x ₁ = 0.0008, x ₂ = 0.0158 using the serial transfer experimental design shown in Fig 1B. The black box denotes the parameter regime for bistability in the model. The circle (red) indicates the inferred parameters based on training set T3.

2. Coupled positive and negative interactions can display robust species coexistence to variations in model parameters. Network diagram (inset) represents the magnitude, sign, and direction of the inferred inter‐species interactions between CH (x ₁) and ER (x ₂). Dashed (gray) and solid (orange) lines indicate a positive and negative interaction, respectively. The line width and node size denote the magnitude of the inter‐species interaction coefficients and steady state abundance of the monospecies, respectively. Heat‐map of the ratio of x ₁ (CH) to x ₂ (ER) at 72 h as a function of the inter‐species interaction coefficients α ₁₂ and α ₂₁. Initial conditions for simulations were x _1o = 0.0008, x _2o = 0.0158. The circle (black) indicates the inferred parameter values for the CH, ER consortium for the gLV model trained on T3.

3. Heat‐map (right) of the ratio of x ₁ to x ₂ at 72 h across a broad range of growth rate parameter values (μ₁ and μ₂). Initial conditions for simulations were x _1o = 0.0008, x _2o = 0.0158. The line (white) outlines the parameter regimes for coexistence and single‐species dominance at steady state. The circle (black) represents the inferred parameter values for the CH, ER consortium.

4. Box plot of the fraction of parameter space that exhibits species coexistence across a range of simulated growth rate parameters for all inferred positive/negative (+/−) or bidirectional negative (−/−) networks for the gLV model trained on T3. Two thousand five hundred combinations of growth rate parameters ranging from 0.05 to 1 h⁻¹ were evaluated. On each box, the red line represents the median, the edges of the box are the 25^th and 75^th percentiles, the whiskers extend to the most extreme data points that the algorithm considers not to be outliers, and the outliers are plotted as red crosses.

Figure 5. Exo‐metabolomics profiling of major metabolites elucidated the metabolic capabilities of monospecies

1. Bipartite network of species (left) and metabolites (right) for metabolites that decreased by at least twofold compared to the abundance of each metabolite at the beginning of the experiment. Colors represent modules containing many overlapping interactions in the network. Network partitioning into modules was performed using BiMat (Flores et al, 2015). Metabolites in bold were depleted and secreted by distinct organisms.

2. Bipartite network of species (left) and metabolites (right) for metabolites that increased in abundance by at least twofold compared to the beginning of the experiment. Metabolites highlighted in bold were depleted or secreted by different species. Colors represent modules containing many overlapping interactions in the network. Network partitioning into modules was performed using BiMat (Flores et al, 2015).

3. Scatter plot of the number of consumed metabolites that decreased by at least twofold compared to the beginning of the experiment vs. the OD600 value of the monospecies culture at the corresponding time point. Error bars represent 1 s.d. from the mean of three biological replicates.

4. Predicted resource utilization interaction network. Each edge represents at least two co‐consumed metabolites that decreased by at least twofold, and the edge width is proportional to the number of co‐consumed metabolites. Node size is proportional to the total number of consumed metabolites for each species.

5. Predicted metabolite interchange network representing metabolites that were secreted or utilized by distinct organisms based on a twofold threshold. Arrows point from the source species to the consumer organism. Node size and line width are proportional to the total number of secreted metabolites and number of predicted metabolite interactions, respectively. Species at the top and bottom of the network are primarily producers or consumers, respectively.