PyPNS: Multiscale Simulation of a Peripheral Nerve in Python
- PMID: 29948844
- PMCID: PMC6394768
- DOI: 10.1007/s12021-018-9383-z
PyPNS: Multiscale Simulation of a Peripheral Nerve in Python
Erratum in
-
Correction to: PyPNS: Multiscale Simulation of a Peripheral Nerve in Python.Neuroinformatics. 2019 Oct;17(4):629. doi: 10.1007/s12021-019-09421-2. Neuroinformatics. 2019. PMID: 30993583 Free PMC article.
Abstract
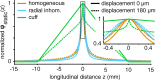
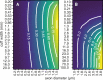
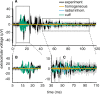
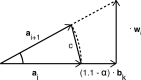
Bioelectronic Medicines that modulate the activity patterns on peripheral nerves have promise as a new way of treating diverse medical conditions from epilepsy to rheumatism. Progress in the field builds upon time consuming and expensive experiments in living organisms. To reduce experimentation load and allow for a faster, more detailed analysis of peripheral nerve stimulation and recording, computational models incorporating experimental insights will be of great help. We present a peripheral nerve simulator that combines biophysical axon models and numerically solved and idealised extracellular space models in one environment. We modelled the extracellular space as a three-dimensional resistive continuum governed by the electro-quasistatic approximation of the Maxwell equations. Potential distributions were precomputed in finite element models for different media (homogeneous, nerve in saline, nerve in cuff) and imported into our simulator. Axons, on the other hand, were modelled more abstractly as one-dimensional chains of compartments. Unmyelinated fibres were based on the Hodgkin-Huxley model; for myelinated fibres, we adapted the model proposed by McIntyre et al. in 2002 to smaller diameters. To obtain realistic axon shapes, an iterative algorithm positioned fibres along the nerve with a variable tortuosity fit to imaged trajectories. We validated our model with data from the stimulated rat vagus nerve. Simulation results predicted that tortuosity alters recorded signal shapes and increases stimulation thresholds. The model we developed can easily be adapted to different nerves, and may be of use for Bioelectronic Medicine research in the future.
Keywords: Bioelectronic medicines; Biophysics; Finite element model; Peripheral nerve; Simulation.
Conflict of interest statement
CH Lubba received funding from Galvani Bioelectronics.
Figures














References
-
- Agudelo-Toro A, Neef A. Computationally efficient simulation of electrical activity at cell membranes interacting with self-generated and externally imposed electric fields. Journal of Neural Engineering. 2013;10(2):1–19. doi: 10.1088/1741-2560/10/2/026019https://doi.org/10.1088/1741-2560/10/2/026019. - DOI - PubMed
-
- Bédard C, Destexhe A. Macroscopic models of local field potentials and the apparent 1/f noise in brain activity. Biophysical Journal. 2009;96(7):2589–2603. doi: 10.1016/j.bpj.2008.12.3951https://doi.org/10.1016/j.bpj.2008.12.3951. - DOI - PMC - PubMed
-
- Birmingham K, Gradinaru V, Anikeeva P, Grill WM, Pikov V, McLaughlin B, Pasricha P, Weber D, Ludwig K, Famm K. Bioelectronic medicines: a research roadmap. Nature Reviews Drug Discovery. 2014;13(6):399–400. doi: 10.1038/nrd4351https://doi.org/10.1038/nrd4351. - DOI - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

