Transmission Dynamics of an SIS Model with Age Structure on Heterogeneous Networks
- PMID: 29948881
- PMCID: PMC7088888
- DOI: 10.1007/s11538-018-0445-z
Transmission Dynamics of an SIS Model with Age Structure on Heterogeneous Networks
Abstract
Infection age is often an important factor in epidemic dynamics. In order to realistically analyze the spreading mechanism and dynamical behavior of epidemic diseases, in this paper, a generalized disease transmission model of SIS type with age-dependent infection and birth and death on a heterogeneous network is discussed. The model allows the infection and recovery rates to vary and depend on the age of infection, the time since an individual becomes infected. We address uniform persistence and find that the model has the sharp threshold property, that is, for the basic reproduction number less than one, the disease-free equilibrium is globally asymptotically stable, while for the basic reproduction number is above one, a Lyapunov functional is used to show that the endemic equilibrium is globally stable. Finally, some numerical simulations are carried out to illustrate and complement the main results. The disease dynamics rely not only on the network structure, but also on an age-dependent factor (for some key functions concerned in the model).
Keywords: Basic reproduction number; Global stability; Infection age; Scale-free network.
Figures
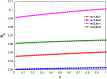

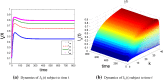
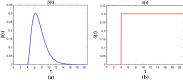
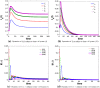
Similar articles
-
Global stability properties of a class of renewal epidemic models.J Math Biol. 2019 May;78(6):1713-1725. doi: 10.1007/s00285-018-01324-1. Epub 2019 Feb 9. J Math Biol. 2019. PMID: 30737545
-
Effect of infection age on an SIS epidemic model on complex networks.J Math Biol. 2016 Nov;73(5):1227-1249. doi: 10.1007/s00285-016-0991-7. Epub 2016 Mar 23. J Math Biol. 2016. PMID: 27007281
-
Epidemic dynamics on semi-directed complex networks.Math Biosci. 2013 Dec;246(2):242-51. doi: 10.1016/j.mbs.2013.10.001. Epub 2013 Oct 17. Math Biosci. 2013. PMID: 24140877
-
Epidemic models for complex networks with demographics.Math Biosci Eng. 2014 Dec;11(6):1295-317. doi: 10.3934/mbe.2014.11.1295. Math Biosci Eng. 2014. PMID: 25365609
-
Dynamics and asymptotic profiles of endemic equilibrium for SIS epidemic patch models.J Math Biol. 2019 Sep;79(4):1279-1317. doi: 10.1007/s00285-019-01395-8. Epub 2019 Jun 29. J Math Biol. 2019. PMID: 31256205
Cited by
-
Data-driven contact structures: From homogeneous mixing to multilayer networks.PLoS Comput Biol. 2020 Jul 16;16(7):e1008035. doi: 10.1371/journal.pcbi.1008035. eCollection 2020 Jul. PLoS Comput Biol. 2020. PMID: 32673307 Free PMC article.
-
Cultural change beyond adoption dynamics: Evolutionary approaches to the discontinuation of contraception.Evol Hum Sci. 2021 Feb 9;3:e13. doi: 10.1017/ehs.2021.8. eCollection 2021. Evol Hum Sci. 2021. PMID: 37588536 Free PMC article. Review.
-
Assessing the impact of disease incidence and immunization on the resilience of complex networks during epidemics.Infect Dis Model. 2024 Sep 12;10(1):1-27. doi: 10.1016/j.idm.2024.08.006. eCollection 2025 Mar. Infect Dis Model. 2024. PMID: 39319286 Free PMC article.
-
Matrix-Based Formulation of Heterogeneous Individual-Based Models of Infectious Diseases: Using SARS Epidemic as a Case Study.Int J Environ Res Public Health. 2021 May 26;18(11):5716. doi: 10.3390/ijerph18115716. Int J Environ Res Public Health. 2021. PMID: 34073465 Free PMC article.
-
Global stability for age-infection-structured human immunodeficiency virus model with heterogeneous transmission.Infect Dis Model. 2024 Feb 7;9(2):437-457. doi: 10.1016/j.idm.2024.01.008. eCollection 2024 Jun. Infect Dis Model. 2024. PMID: 38385020 Free PMC article.
References
-
- Adams RA, Fournier JJF. Sobolev spaces. 2. Amsterdam: Elsevier; 2003.
-
- Anderson RM, May RM. Infectious diseases of humans. Oxford: Oxford University Press; 1991.
-
- Bailey NTJ. The mathematical theory of infectious diseases and its applications. 2. New York: Hafner; 1975.
-
- Browne CJ, Pilyugin SS. Global analysis of age-structured within-host virus model. Discrete Contin Dyn Syst: Ser B. 2013;18(8):1999–2017. doi: 10.3934/dcdsb.2013.18.1999. - DOI
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

