Exploring the Tiers of Rooted Phylogenetic Network Space Using Tail Moves
- PMID: 29948885
- PMCID: PMC6061524
- DOI: 10.1007/s11538-018-0452-0
Exploring the Tiers of Rooted Phylogenetic Network Space Using Tail Moves
Abstract
Popular methods for exploring the space of rooted phylogenetic trees use rearrangement moves such as rooted Nearest Neighbour Interchange (rNNI) and rooted Subtree Prune and Regraft (rSPR). Recently, these moves were generalized to rooted phylogenetic networks, which are a more suitable representation of reticulate evolutionary histories, and it was shown that any two rooted phylogenetic networks of the same complexity are connected by a sequence of either rSPR or rNNI moves. Here, we show that this is possible using only tail moves, which are a restricted version of rSPR moves on networks that are more closely related to rSPR moves on trees. The connectedness still holds even when we restrict to distance-1 tail moves (a localized version of tail moves). Moreover, we give bounds on the number of (distance-1) tail moves necessary to turn one network into another, which in turn yield new bounds for rSPR, rNNI and SPR (i.e. the equivalent of rSPR on unrooted networks). The upper bounds are constructive, meaning that we can actually find a sequence with at most this length for any pair of networks. Finally, we show that finding a shortest sequence of tail or rSPR moves is NP-hard.
Keywords: Diameter; Head-move operation; Network space; Phylogenetic network; Rearrangement; Tail-move operation.
Figures


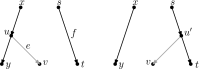
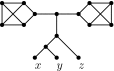

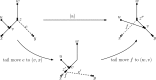










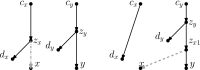



Similar articles
-
Rearrangement moves on rooted phylogenetic networks.PLoS Comput Biol. 2017 Aug 1;13(8):e1005611. doi: 10.1371/journal.pcbi.1005611. eCollection 2017 Aug. PLoS Comput Biol. 2017. PMID: 28763439 Free PMC article.
-
Lost in space? Generalising subtree prune and regraft to spaces of phylogenetic networks.J Theor Biol. 2017 Jun 21;423:1-12. doi: 10.1016/j.jtbi.2017.03.032. Epub 2017 Apr 13. J Theor Biol. 2017. PMID: 28414085
-
A polynomial-time algorithm computing lower and upper bounds of the rooted subtree prune and regraft distance.J Comput Biol. 2011 May;18(5):743-57. doi: 10.1089/cmb.2010.0045. Epub 2010 Dec 18. J Comput Biol. 2011. PMID: 21166560
-
Classes of explicit phylogenetic networks and their biological and mathematical significance.J Math Biol. 2022 May 3;84(6):47. doi: 10.1007/s00285-022-01746-y. J Math Biol. 2022. PMID: 35503141 Review.
-
A review of metrics measuring dissimilarity for rooted phylogenetic networks.Brief Bioinform. 2019 Nov 27;20(6):1972-1980. doi: 10.1093/bib/bby062. Brief Bioinform. 2019. PMID: 30020404 Review.
Cited by
-
Advancing admixture graph estimation via maximum likelihood network orientation.Bioinformatics. 2021 Jul 12;37(Suppl_1):i142-i150. doi: 10.1093/bioinformatics/btab267. Bioinformatics. 2021. PMID: 34252951 Free PMC article.
-
The Space of Equidistant Phylogenetic Cactuses.Ann Comb. 2024;28(1):1-32. doi: 10.1007/s00026-023-00656-0. Epub 2023 Jun 9. Ann Comb. 2024. PMID: 38433929 Free PMC article.
-
Spaces of ranked tree-child networks.J Math Biol. 2025 Sep 2;91(3):32. doi: 10.1007/s00285-025-02265-2. J Math Biol. 2025. PMID: 40892068 Free PMC article.
-
Generating normal networks via leaf insertion and nearest neighbor interchange.BMC Bioinformatics. 2019 Dec 17;20(Suppl 20):642. doi: 10.1186/s12859-019-3209-3. BMC Bioinformatics. 2019. PMID: 31842746 Free PMC article.
-
Exploring spaces of semi-directed level-1 networks.J Math Biol. 2023 Oct 13;87(5):70. doi: 10.1007/s00285-023-02004-5. J Math Biol. 2023. PMID: 37831304 Free PMC article.
References
-
- Atkins R, McDiarmid C (2015) Extremal distances for subtree transfer operations in binary trees. arXiv preprint arXiv:1509.00669
-
- Bordewich M, Semple C. On the computational complexity of the rooted subtree prune and regraft distance. Ann Comb. 2005;8(4):409–423. doi: 10.1007/s00026-004-0229-z. - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

