Chunking as a rational strategy for lossy data compression in visual working memory
- PMID: 29952621
- PMCID: PMC6026019
- DOI: 10.1037/rev0000101
Chunking as a rational strategy for lossy data compression in visual working memory
Abstract
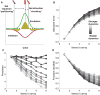
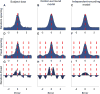
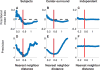
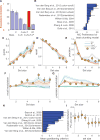
The nature of capacity limits for visual working memory has been the subject of an intense debate that has relied on models that assume items are encoded independently. Here we propose that instead, similar features are jointly encoded through a "chunking" process to optimize performance on visual working memory tasks. We show that such chunking can: (a) facilitate performance improvements for abstract capacity-limited systems, (b) be optimized through reinforcement, (c) be implemented by center-surround dynamics, and (d) increase effective storage capacity at the expense of recall precision. Human performance on a variant of a canonical working memory task demonstrated performance advantages, precision detriments, interitem dependencies, and trial-to-trial behavioral adjustments diagnostic of performance optimization through center-surround chunking. Models incorporating center-surround chunking provided a better quantitative description of human performance in our study as well as in a meta-analytic dataset, and apparent differences in working memory capacity across individuals were attributable to individual differences in the implementation of chunking. Our results reveal a normative rationale for center-surround connectivity in working memory circuitry, call for reevaluation of memory performance differences that have previously been attributed to differences in capacity, and support a more nuanced view of visual working memory capacity limitations: strategic tradeoff between storage capacity and memory precision through chunking contribute to flexible capacity limitations that include both discrete and continuous aspects. (PsycINFO Database Record
(c) 2018 APA, all rights reserved).
Conflict of interest statement
The authors declare no competing interests.
Figures

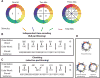
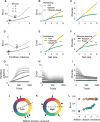
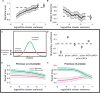
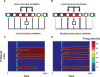

References
-
- Almeida R, Barbosa J, Compte A. Neural circuit basis of visuo-spatial working memory precision: a computational and behavioral study. Journal of Neurophysiology. 2015;114(3):1806–1818. http://doi.org/10.1152/jn.00362.2015. - DOI - PMC - PubMed
-
- Barak O, Sussillo D, Romo R, Tsodyks M, Abbott LF. From fixed points to chaos: Three models of delayed discrimination. Progress in Neurobiology. 2013;103:214–222. http://doi.org/10.1016/j.pneurobio.2013.02.002. - DOI - PMC - PubMed
-
- Bays PM, Husain M. Dynamic shifts of limited working memory resources in human vision. Science. 2008;321(5890):851–854. http://doi.org/10.1126/science.1158023. - DOI - PMC - PubMed
-
- Bays PM, Catalao RFG, Husain M. The precision of visual working memory is set by allocation of a shared resource. Journal of Vision. 2009;9(10):7.1–11. http://doi.org/10.1167/9.10.7. - DOI - PMC - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

