Subgroup identification in clinical trials: an overview of available methods and their implementations with R
- PMID: 29955582
- PMCID: PMC6015941
- DOI: 10.21037/atm.2018.03.07
Subgroup identification in clinical trials: an overview of available methods and their implementations with R
Abstract
Randomized controlled trials (RCTs) usually enroll heterogeneous study population, and thus it is interesting to identify subgroups of patients for whom the treatment may be beneficial or harmful. A variety of methods have been developed to do such kind of post hoc analyses. Conventional generalized linear model is able to include prognostic variables as a main effect and predictive variables in an interaction with treatment variable. A statistically significant and large interaction effect usually indicates potential subgroups that may have different responses to the treatment. However, the conventional regression method requires to specify the interaction term, which requires knowledge of predictive variables or becomes infeasible when there is a large number of feature variables. The Least Absolute Shrinkage and Selection Operator (LASSO) method does variable selection by shrinking less clear effects (including interaction effects) to zero and in this way selects only certain variables and interactions for the model. There are many tree-based methods for subgroup identification. For example, model-based recursive partitioning incorporates parametric models such as generalized linear models into trees. The model incorporated is usually a simple model with only the treatment as covariate. Predictive and prognostic variables are found and incorporated automatically via the tree. The present article gives an overview of these methods and explains how to perform them using the free software environment for statistical computing R (version 3.3.2). A simulated dataset is employed for illustrating the performance of these methods.
Keywords: Subgroup; classification tree; lasso; recursive partitioning; regression tree.
Conflict of interest statement
Conflicts of Interest: The authors have no conflicts of interest to declare.
Figures
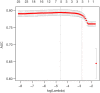
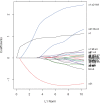



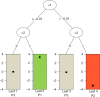

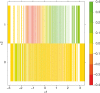
References
-
- Kehl V, Ulm K. Responder identification in clinical trials with censored data. Computational Statistics & Data Analysis 2006;50:1338-55. 10.1016/j.csda.2004.11.015 - DOI
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources
