Immediate action is the best strategy when facing uncertain climate change
- PMID: 29967461
- PMCID: PMC6028488
- DOI: 10.1038/s41467-018-04968-1
Immediate action is the best strategy when facing uncertain climate change
Abstract
Mitigating the detrimental effects of climate change is a collective problem that requires global cooperation. However, achieving cooperation is difficult since benefits are obtained in the future. The so-called collective-risk game, devised to capture dangerous climate change, showed that catastrophic economic losses promote cooperation when individuals know the timing of a single climatic event. In reality, the impact and timing of climate change is not certain; moreover, recurrent events are possible. Thus, we devise a game where the risk of a collective loss can recur across multiple rounds. We find that wait and see behavior is successful only if players know when they need to contribute to avoid danger and if contributions can eliminate the risks. In all other cases, act quickly is more successful, especially under uncertainty and the possibility of repeated losses. Furthermore, we incorporate influential factors such as wealth inequality and heterogeneity in risks. Even under inequality individuals should contribute early, as long as contributions have the potential to decrease risk. Most importantly, we find that catastrophic scenarios are not necessary to induce such immediate collective action.
Conflict of interest statement
The authors declare no competing interests.
Figures

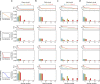

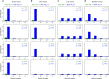
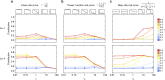
References
-
- Schmidt RC. A balanced-efforts approach for climate cooperation. Nat. Clim. Change. 2015;50:10–12. doi: 10.1038/nclimate2447. - DOI
-
- Ordner JP. Community action and climate change. Nat. Clim. Change. 2017;70:161–163. doi: 10.1038/nclimate3236. - DOI
-
- Gordon HS. The economic theory of a common-property resource: the fishery. J. Polit. Econ. 1954;62:124–142. doi: 10.1086/257497. - DOI
-
- Hardin R. Collective action as an agreeable n-prisoners’ dilemma. Behav. Sci. 1971;160:472–481. doi: 10.1002/bs.3830160507. - DOI
LinkOut - more resources
Full Text Sources
Other Literature Sources

