Local structure can identify and quantify influential global spreaders in large scale social networks

Abstract

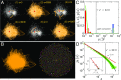
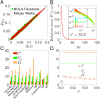
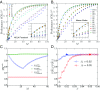
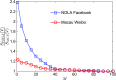
Measuring and optimizing the influence of nodes in big-data online social networks are important for many practical applications, such as the viral marketing and the adoption of new products. As the viral spreading on a social network is a global process, it is commonly believed that measuring the influence of nodes inevitably requires the knowledge of the entire network. Using percolation theory, we show that the spreading process displays a nucleation behavior: Once a piece of information spreads from the seeds to more than a small characteristic number of nodes, it reaches a point of no return and will quickly reach the percolation cluster, regardless of the entire network structure; otherwise the spreading will be contained locally. Thus, we find that, without the knowledge of the entire network, any node's global influence can be accurately measured using this characteristic number, which is independent of the network size. This motivates an efficient algorithm with constant time complexity on the long-standing problem of best seed spreaders selection, with performance remarkably close to the true optimum.

Keywords: complex network; influence; percolation; social media; viral marketing.

Fig. 1.

Two phases phenomena. (A) Examples of simulated local (1, 3, 5) and viral (2, 4, 6) SIR spreadings in the NOLA Facebook network ($\beta =0.02,{\beta }_c=0.01$). We start the simulation from a randomly chosen node (red, $k=27$). The active and nonactive nodes are colored in orange and white, respectively. (B) An illustration of giant (Left) and finite (Right) clusters in a bond percolation process. (C) The spreading probability distribution $g\left(i,s\right)$ (columns) is plotted together with the cluster size distribution function $p\left(s\right)$ (green line) obtained from percolation. Note that $p\left(s\right)$ is the average of $g\left(i,s\right)$ over all nodes. In this example, we use the same seed node $i$ as in A, but other randomly chosen nodes give similar bimodal distributions, with the same viral peak at $s^{\infty }$ (SI Appendix, section II). (D) The finite part $p_{\mathrm{f}}\left(s\right)$ (green circles) of $p\left(s\right)$ is fitted to Eq. 5 (black solid line) to obtain the characteristic size $s*=32.9\pm 0.6$ and the exponent $\tau =2.50$. (D, Inset) The characteristic size $s*$ is fitted to a power-law divergence near the critical point ${\beta }_c$, with a non–mean-field exponent $\sigma =1.05$. The same network and the same $\beta$ are used in A–D.

Fig. 2.

Spreading power. (A) Comparison between the truncated spreading power $\tilde{S}\left(i\right)$ (Eq. 4) and the real exact spreading power $S\left(i\right)$ (Eq. 1) in NOLA Facebook and Macau Weibo (${\beta }_c=0.05$) networks, where each point represents one node. (B) The $m$ dependence of the relative error $E^{\mathrm{r}}\left(i,m\right)$ of nodes whose degrees are equal to the average degree $⟨k⟩$, in the NOLA Facebook ($\beta =0.02$) network. (B, Inset) The $m$ dependence of the relative error $E^{\mathrm{r}}\left(i,m\right)$ of nodes with different degrees. The relative error decreases quickly with $m$ and becomes smaller than $1\%$ when $m>s*$. (C) Comparison among the influence radius $\ell *$, the average distance of the farthest nodes from the seed nodes ${\ell }_{\infty }*$, and the network diameter $D$ in nine OSNs and two random networks [an ER network with $N=\mathrm{50,000},⟨k⟩=10$ and a scale-free (SF) network with $N=\mathrm{50,000},P\left(k\right)\sim k^{-2.5}$]. We choose $\beta$ in different networks such that the fraction of the giant component is the same; i.e., $s^{\infty }=0.3N$ (see SI Appendix, section I for the real networks description). (D) The NOLA Facebook influence radius $\ell *$ is smaller than both ${\ell }_{\infty }*$ and $D$ for any $\beta >{\beta }_c$.

Fig. 3.

Algorithm time complexity. (A) Comparison of the computational execution count of percolation-based greedy algorithm(PBGA) and natural greedy algorithm (NGA) (8) in ER networks with $\beta =0.2$ (${\beta }_c=0.1$). The algorithms select the set of $M=10$ most influential nodes from $L=\mathrm{1,000}$ candidates with degree at $⟨k⟩=10$. Unlike the NGA, PBGA’s computational complexities are independent of network size. (B) Comparison of the computational execution count (rescaled by $⟨k⟩$ and $m$) of the same algorithms in real OSNs (open symbols, from left to right: CA-GrQc, CA-HepTh, Macau Weibo, Email-Enron, NOLA Facebook, DBLP, Delicious, QQ, and LiveJournal; see SI Appendix, section I for the real networks description). The solid symbols are values of extrapolated execution count based on the size of whole Twitter and Facebook networks. The value of $\beta$ is chosen such that the giant component size is 30% of the network size; i.e., $s^{\infty }=0.3N$ in each OSN.

Fig. 4.

Algorithm performance on real online social networks. For (A) NOLA Facebook ($\beta =0.012$) and (B) Macau Weibo ($\beta =0.055$) networks, we compare the algorithm performance of the PBGA with that of other algorithms: brute-force search (BFS), degree discount heuristic (DDH) (8), eigenvector method (EM), genetic algorithm (GA), maximum betweenness (MB) (10), maximum closeness (MC) (11), maximum degree (MD), maximum Katz (MK) index (12), maximum k-shell (MKS) (2), NGA, and MCI (4). The candidate nodes are randomly selected from the nodes with median degree nodes: Degree is 10 for nodes in Facebook and out-degree is 3 for nodes from Weibo. Since the candidate nodes have the same degree, the MD method is equivalent to the random selection of seed nodes. $S\left(\mathcal{V}\right)$ is normalized by dividing the giant component size $s^{\infty }$. Here $L=100$ candidates and $M$ varies from 1 to 100. (A and B, Insets) The regime $1\le M\le 6$ is enlarged, where the rigorous optimum obtained from BFS is available. (C) On the Facebook network, the combined rigorous lower bound ${\mathrm{P}\mathrm{R}}_{\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{b}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$ and the approximated lower bound ${\mathrm{P}\mathrm{R}}_{\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{x}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$ are plotted together with the submodular lower bound ${\mathrm{P}\mathrm{R}}_{\mathrm{s}\mathrm{u}\mathrm{b}\mathrm{m}\mathrm{o}\mathrm{d}}^{\mathrm{m}\mathrm{i}\mathrm{n}}=0.63$ (17), as functions of $M$. (D) The relative performance between the PBGA solution based on $\beta =0.02$ ($\beta =0.05$) and the PBGA solution based on the other $\beta$ values, with both performances ${\tilde{\mathcal{V}}}_0$ and ${\tilde{\mathcal{V}}}_{\beta }$ estimated upon the same spreading rate $\beta$. The solid symbols (blue star and red diamond) label the performance of 1 when $\beta ={\beta }_0$. We see that as long as $\beta >{\beta }_0$, the solution at ${\beta }_0$ can be used at $\beta$ since their performances are almost the same, as long as both ${\beta }_0$ and $\beta$ are larger than the critical point ${\beta }_c\approx 0.01$.

Fig. 5.

Performance comparison between the PBGA and MCI. The vertical axis is the ratio between the seeds’ influence of the PBGA and MCI. For a small number $M$ of seed nodes, the PBGA significantly outperforms MCI. The difference diminishes as $M$ increases, when both solutions approach the theoretical maximum of giant component size. The simulation is carried out on the Facebook network with $\beta =0.012$.