Electric Fields Elicit Ballooning in Spiders

Abstract

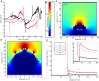
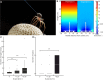
When one thinks of airborne organisms, spiders do not usually come to mind. However, these wingless arthropods have been found 4 km up in the sky [1], dispersing hundreds of kilometers [2]. To disperse, spiders "balloon," whereby they climb to the top of a prominence, let out silk, and float away. The prevailing view is that drag forces from light wind allow spiders to become airborne [3], yet ballooning mechanisms are not fully explained by current aerodynamic models [4, 5]. The global atmospheric electric circuit and the resulting atmospheric potential gradient (APG) [6] provide an additional force that has been proposed to explain ballooning [7]. Here, we test the hypothesis that electric fields (e-fields) commensurate with the APG can be detected by spiders and are sufficient to stimulate ballooning. We find that the presence of a vertical e-field elicits ballooning behavior and takeoff in spiders. We also investigate the mechanical response of putative sensory receivers in response to both e-field and air-flow stimuli, showing that spider mechanosensory hairs are mechanically activated by weak e-fields. Altogether, the evidence gathered reveals an electric driving force that is sufficient for ballooning. These results also suggest that the APG, as additional meteorological information, can reveal the auspicious time to engage in ballooning. We propose that atmospheric electricity adds key information to our understanding and predictive capability of the ecologically important mass migration patterns of arthropod fauna [8]. VIDEO ABSTRACT.

Keywords: atmospheric potential gradient; ballooning; electrostatics; mechanoreception; sensory ecology; spider; trichobothria.

Figure 1

Quantifying Electric Fields in Nature (A) Atmospheric potential gradient (APG) measured for 30 min periods across 3 days using a field mill (Chillworth JCI131) at the University of Bristol School of Veterinary Sciences, Langford. Colors depict recordings from different days in June 2016. (B) Scale bar for (C) and (D). (C) Finite element analysis (FEA) model of electric field (e-field) enhancement around a geometrically domed oak tree in an APG strength of 4 kVm⁻¹. (D) FEA model detailing the e-field around geometrically sharp tree branches in an APG strength of 4 kVm⁻¹. (E) Two-dimensional plot of the e-field along cut lines (red; left inset) of (C) oak modeled as geometrically domed (solid) and (D) branches (dashed) in an APG of 4 kVm⁻¹ (red) and 1 kVm⁻¹ (black). Inset: detail of area indicated by the gray box. See also Figure S1.

Figure 2

Spider Ballooning Behavior (A) A spider showing a typical tiptoe stance. (B) Finite element model of the electric potential (left) and e-field (right) in the behavioral arena. The electric potential is the potential energy required to move a charge from one place to another without producing any acceleration: the amount of work per unit charge. It is a scalar quantity. The electric field is a vector quantity and a force that surrounds an electric charge. It exerts either an attractive or repelling force on other charges. The base is modeled as ground with 5,000 V applied to the top plate. A water moat surrounds the takeoff site to prevent spiders escaping over ground. The water was electrically floating, not connected to ground or a voltage. The scale bar shows electric potential (left) and e-field (right). Aside from small areas around the base of the arena, the e-field is fairly uniform with a strength of 6.25 kVm⁻¹ (blue color indicated on the scale bar). (C and D) Boxplots showing the (C) number of dragline drops in response to 1.25 kVm⁻¹, 6.25 kVm⁻¹, and zero-voltage control and (D) the number of tiptoes in response to 1.25 kVm⁻¹, 6.25 kVm⁻¹ and zero-voltage control (D). Significance levels: ^∗∗∗p < 0.001, ^∗∗p < 0.01. See also Video S1 and Table S1.

Figure 3

Mechanical Displacement of Spider Trichobothria Trichobothria in Erigone. (A) Diagram of a spider illustrating locations of metatarsal trichobothria and locations for non-contact laser Doppler vibrometry measurement (stars). (B) Scanning electron microscopy image of adult male Erigone metatarsi and trichobothria, with a close-up view of trichobothrium (inset). Arrows point to the base of trichobothrium. MT, metatarsus; T, tarsus. (C–H) Displacement of trichobothria in response to 0.5 ms⁻¹ air flow (C and D), pseudo-DC efield (E and F), and 1 Hz sine e-field (G and H) measured using laser Doppler vibrometry (LDV). (C), (E), and (G) show single traces, and (D), (F), and (H) show the mean (black) and SD (gray). n = 6 (D), n = 5 (F), and n = 4 (H). Gray dashed lines indicate the stimulus.

Figure 4

Velocity of Trichobothria Motion in Response to E-Fields (A) Transient changes in velocity of a trichobothrium (black, solid line) in response to a 2 kVm⁻¹¹ e-field oscillating at 0.1 Hz (gray, dashed line). (B) Transient changes in velocity of a metatarsal spine (black, solid line) in response to a 3.6 kVm⁻¹¹ e-field oscillating at 0.1 Hz (gray, dashed line). (C) Spike rate (as seen in A and B) of trichobothria (black; n = 8; ±SD) and metatarsal spine (gray; n = 4; ±SD) across a range of e-field strengths. Spike rate was measured as the ratio between the total number of zero crossing of the e-field stimulus to the number of spikes coincident (within 25 ms) of stimulus zero crossings. (D) Histogram (binned every 25 ms) of the number of velocity spikes of the trichobothria (black; n = 8) and metatarsal spines (white; n = 4) in response to a 0.1 Hz square wave. The dashed gray line shows stimulus recording. (E) Velocity of a trichobothrium (black, solid line) in response to an e-field oscillating at 1 Hz (gray, dashed line). (F) Frequency response (FFT) of trichobothria (black; n = 6; ±SD) in response to a 1 Hz sine wave e-field.