Branch/mode competition in the flow-induced vibration of a square cylinder

Abstract

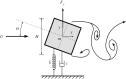
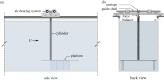
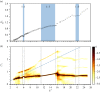
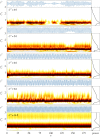
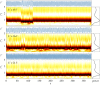
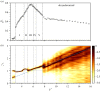
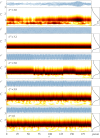
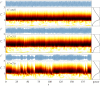
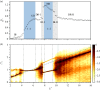
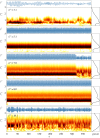
The flow-induced vibration response of a square cross-sectional cylinder with low mass and damping ratio is analysed using continuous wavelet transforms (CWT) for three representative angles of attack of the cylinder to the incoming flow. The amplitude and frequency responses over a range of flow velocities map out multiple regimes (branches) of oscillation. Analysis of the time-frequency domain for boundary regions between branches using CWT reveals intermittency at the synchronization region boundaries as well as mode competition at branch boundaries. Complementary recurrence analysis shows that periodic dynamical states are interrupted by chaotic bursts in the transition regions around the higher branch at an angle of attack of α = 20° (a new branch first observed by Nemes et al. (2012 J. Fluid Mech.710, 102-130 (doi:10.1017/jfm.2012.353))), supporting the CWT-based frequency-time analysis.This article is part of the theme issue 'Redundancy rules: the continuous wavelet transform comes of age'.

Keywords: bluff body; flow-induced vibration; fluid–structure interaction; wavelet.

Figure 1.

A definition sketch of the problem studied—a square cross section with variable angle of attack, α, constrained to oscillate across the stream.

Figure 2.

A schematic showing the experimental set-up in the test section of the water channel. (Online version in colour.)

Figure 3.

The normalized amplitude response and the logarithmic-scale frequency power spectral density (PSD) contours as a function of the reduced velocity for α = 0°. Note that the frequency PSD contours here are constructed by stacking the frequency PSD based on short-time Fourier transforms (STFT) at each U* [6]. The 1 : 1, 1 : 3 and 1 : 5 synchronization regimes are highlighted with blue shading in (a), and their boundaries are illustrated by the vertical dashed lines in (b). The dotted-dashed slope line represents the Strouhal number St≃0.131 (measured in the fixed cylinder case). (Online version in colour.)

Figure 4.

Time series of the normalized (measured) cylinder displacement along with the frequency energy contours based on CWT at various U* values for α = 0°. Note that y* denotes the normalized body position from its neutral position at zero flow velocity; τ = f_nwt is the normalized time. (Online version in colour.)

Figure 5.

Time series of the normalized cylinder displacement along with the frequency energy contours based on CWT at various U* values for α = 0° (continued from figure 4). (Online version in colour.)

Figure 6.

The amplitude and frequency responses as a function of U* for α = 45°. Five regimes (I–V) are identified within the VIV lock-in region. In (b), the dotted-dashed slope line represents the Strouhal number St≃0.176. Note that the frequency PSD contours here are constructed based on STFT analysis [6]. (Online version in colour.)

Figure 7.

Time series of the normalized cylinder displacement along with the frequency energy contours based on CWT at various U* values for α = 45°. (Online version in colour.)

Figure 8.

Time series of the normalized cylinder displacement along with the frequency energy contours based on CWT at various U* values for α = 45° (continued from figure 7). (Online version in colour.)

Figure 9.

The amplitude response and the logarithmic-scale frequency PSD contours as a function of the reduced velocity for the case of α = 20°. The 1 : 1 and 1 : 2 synchronization regimes are highlighted with blue shading in (a). Two intermittency regions (IR-I and IR-II) are highlighted with grey shading. In (b), the vertical dashed lines illustrate the boundaries of the regimes. The dotted-dashed line represents the Strouhal number St≃0.176. Note that the frequency PSD contours here are constructed based on STFT analysis [6]. (Online version in colour.)

Figure 10.

Time series of the normalized cylinder displacement along with the frequency energy contours based on CWT at various U* values for α = 20°. (Online version in colour.)

Figure 11.

Recurrence plots (lower) of the time series of the normalized body displacement (upper) for the case of α = 20° showing different dynamical states in different response regimes: (a) periodic state at U* = 5.1 (UB), (b) periodic and transient chaotic states at U* = 7.8 (IR-I), (c) periodic state at U* = 8.0 (HB) and (d) periodic and transient chaotic states at U* = 10.1 (IR-II). (Online version in colour.)