Separated-pair approximation and separated-pair pair-density functional theory

Abstract

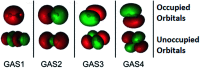
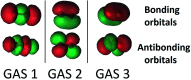
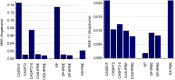
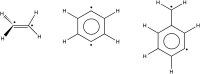
Multi-configuration pair-density functional theory (MC-PDFT) has proved to be a powerful way to combine the capabilities of multi-configuration self-consistent-field theory to represent the an electronic wave function with a highly efficient way to include dynamic correlation energy by density functional theory. All applications reported previously involved complete active space self-consistent-field (CASSCF) theory for the reference wave function. For treating large systems efficiently, it is necessary to ask whether good accuracy is retained when using less complete configuration interaction spaces. To answer this question, we present here calculations employing MC-PDFT with the separated pair (SP) approximation, which is a special case (defined in this article) of generalized active space self-consistent-field (GASSCF) theory in which no more than two orbitals are included in any GAS subspace and in which inter-subspace excitations are excluded. This special case of MC-PDFT will be called SP-PDFT. In SP-PDFT, the electronic kinetic energy and the classical Coulomb energy, the electronic density and its gradient, and the on-top pair density and its gradient are obtained from an SP approximation wave function; the electronic energy is then calculated from the first two of these quantities and an on-top density functional of the last four. The accuracy of the SP-PDFT method for predicting the structural properties and bond dissociation energies of twelve diatomic molecules and two triatomic molecules is compared to the SP approximation itself and to CASSCF, MC-PDFT based on CASSCF, CASSCF followed by second order perturbation theory (CASPT2), and Kohn-Sham density functional theory with the PBE exchange-correlation potential. We show that SP-PDFT reproduces the accuracy of MC-PDFT based on the corresponding CASSCF wave function for predicting C-H bond dissociation energies, the reaction barriers of pericyclic reactions and the properties of open-shell singlet systems, all at only a small fraction of the computational cost.

Fig. 1. The four GAS subspaces used in the SP-4 approximation for the carbon dimer, C₂. In this scheme, the 2s, 2p_z, 2p_x, and 2p_y atomic orbitals form σ_g, σ_u, π(p_x), and π(p_y) (which are bonding or in the case of 2σ_u, GAS2, antibonding) orbitals respectively as well as their antibonding (or in the case of 2σ_u, GAS2, bonding) counterparts. These pairs are shown from left to right. The orbitals with an occupation close to two are placed at the top, while those that are nearly empty are placed at the bottom. Two electrons are placed in each GAS subspace. Intra-space excitations (up to double excitations) between a bonding orbital and its antibonding pair are allowed. Inter-subspace excitations between GAS subspaces are not allowed.

Fig. 2. The three GAS subspaces used in SP calculations on triplet dioxygen, O₂. In this scheme, the 2p_z atomic orbitals form 3σ and 3σ* orbitals, and the 2p_x and 2p_y atomic orbitals form bonding π(p_x), and π(p_y) orbitals and correlating antibonding π*(p_x), and π*(p_y) orbitals. These are shown from left to right. GAS 1 contains two electrons while GAS 2 and GAS 3 each contain 3 electrons. Inter-subspace excitations between GAS spaces are not allowed.

Fig. 3. Mean absolute errors (MAE) with respect to experimental values of the calculated bond distances of eleven main-group diatomic molecules and the chromium dimer, Cr₂, obtained with several computational approaches (left). The MAE obtained without the results for Cr₂ (labeled as MAE-11) is shown on the right. The theoretical methods are grouped into three classes. The first are based on CASSCF (CASSCF, CASPT2, CASPT2-0, CAS-tPBE, CAS-ftPBE). The second are based on the SP approximation (SP, SP-tPBE, SP-ftPBE). The third is Kohn–Sham DFT with the PBE exchange–correlation functional. All experimental data were obtained from ref. 40.

Fig. 4. Illustrative descriptions of the CAS and SP active spaces used in CASSCF and SP calculations on ³B₁ CH₂ (left) and O₃ (right). Refer to the text for the full descriptions of the active spaces used in the CASSCF and SP calculations.

Fig. 5. Illustrative descriptions of the CAS and SP active spaces used in CASSCF and SP calculations on: ethane (top) and the ethyl radical (bottom). Notice that the C–C orbitals are not included in SP subspaces as we are concerned only with C–H bond dissociation.

Fig. 6. The barriers for these five pericyclic reactions were calculated with SP-PDFT and other theoretical methods.

Fig. 7. Illustrations of the structures of twisted ethylene, 1,4-didehydrobenzene and α,3-didehydrotoluene.