Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Review
. 2018 Jul 2;18(7):2120.
doi: 10.3390/s18072120.

A Comparative Study of Four Kinds of Adaptive Decomposition Algorithms and Their Applications

Tao Liu  1   2 , Zhijun Luo  3 , Jiahong Huang  4 , Shaoze Yan  5
Affiliations
Review

A Comparative Study of Four Kinds of Adaptive Decomposition Algorithms and Their Applications

Tao Liu et al. Sensors (Basel). .

Abstract

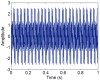
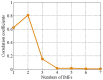
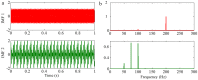
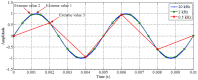
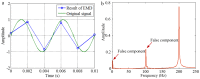
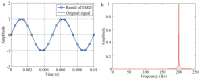
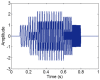
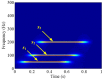
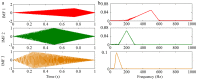
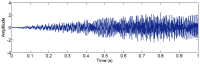
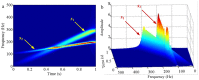
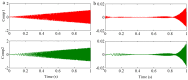
The adaptive decomposition algorithm is a powerful tool for signal analysis, because it can decompose signals into several narrow-band components, which is advantageous to quantitatively evaluate signal characteristics. In this paper, we present a comparative study of four kinds of adaptive decomposition algorithms, including some algorithms deriving from empirical mode decomposition (EMD), empirical wavelet transform (EWT), variational mode decomposition (VMD) and Vold⁻Kalman filter order tracking (VKF_OT). Their principles, advantages and disadvantages, and improvements and applications to signal analyses in dynamic analysis of mechanical system and machinery fault diagnosis are showed. Examples are provided to illustrate important influence performance factors and improvements of these algorithms. Finally, we summarize applicable scopes, inapplicable scopes and some further works of these methods in respect of precise filters and rough filters. It is hoped that the paper can provide a valuable reference for application and improvement of these methods in signal processing.

Keywords: adaptive decomposition algorithm; narrow-band signal; non-stationary signal; signal processing.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflicts of interest.

Figures

Figure 1
Figure 1
The waveform of the sample signal fsig1 between in time domain.
Figure 2
Figure 2
The coefficients of correlation different IMFs and the sample signal.
Figure 3
Figure 3
The waveforms of the IMFs 1 and 2 of fsig1 and the corresponding Fourier spectrums: (a) waveforms and (b) Fourier spectrums.
Figure 4
Figure 4
The distributions of extreme values of a signal of 200 Hz with sampling frequencies of 0.5, 2 and 20 kHz.
Figure 5
Figure 5
The EMD result of the signal of 200 Hz with a sampling frequency of 0.5 kHz and the corresponding Fourier spectrum: (a) the results of EMD and (b) the Fourier spectrum.
Figure 6
Figure 6
The EMD result of the signal of 200 Hz with a sampling frequency of 2 kHz and the corresponding Fourier spectrum: (a) the result of EMD and (b) the Fourier spectrum.
Figure 7
Figure 7
The waveform of the sample signal fsig2 in time domain.
Figure 8
Figure 8
The STFT of the sample signal fsig2.
Figure 9
Figure 9
The coefficients of correlation between different IMFs and the sample signal fsig2.
Figure 10
Figure 10
The waveforms of the IMFs 1–3.
Figure 11
Figure 11
The ideal time-frequency distributions of the IMFs 1–3: (a) IMF 1; (b) IMF 2 and (c) IMF 3.
Figure 12
Figure 12
The STFT representations of the IMFs 1–3: (a) IMF 1; (b) IMF 2 and (c) IMF 3.
Figure 13
Figure 13
The waveforms of the IMFs 1–3 and the corresponding Fourier spectrums: (a) waveforms and (b) Fourier spectrums.
Figure 14
Figure 14
The waveforms of the IMFs 1–3 of fsig1 and the corresponding Fourier spectrums: (a) waveforms and (b) Fourier spectrums.
Figure 15
Figure 15
The EEMD result of the signal of 200 Hz with a sampling frequency of 2 kHz and the corresponding Fourier spectrum: (a) the result of EEMD and (b) the Fourier spectrum.
Figure 16
Figure 16
The waveform of the sample signal fsig3.
Figure 17
Figure 17
The waveforms of the IMFs 1–3 of fsig3 by EEMD and CEEMD: (a) EEMD and (b) CEEMD.
Figure 18
Figure 18
Residues of added white noises derived by EEMD and CEEMD: (a) EEMD and (b) CEEMD.
Figure 18
Figure 18
Residues of added white noises derived by EEMD and CEEMD: (a) EEMD and (b) CEEMD.
Figure 19
Figure 19
The waveform of the sample signal fsig4.
Figure 20
Figure 20
Comparisons among EMD, EEMD, CEEMD and improved CEEMDAN.
Figure 21
Figure 21
The errors of decomposition results of EEMD, CEEMD and improved CEEMDAN.
Figure 22
Figure 22
Segmenting Fourier spectrum into N contiguous segments.
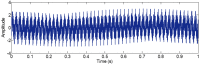
Figure 23
Figure 23
The waveform of the sample signal fsig5.
Figure 24
Figure 24
The waveforms of EWT result of fsig5 and the corresponding Fourier spectrums: (a) waveforms and (b) Fourier spectrums.
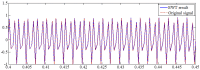
Figure 25
Figure 25
The EWT result and the original signal of 800 Hz within [0.4 0.45] s.
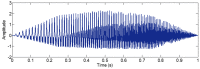
Figure 26
Figure 26
The waveform of the sample signal fsig6.
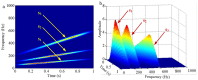
Figure 27
Figure 27
The STFT of the sample signal fsig6: (a) 2D figure and (b) 3D figure.
Figure 28
Figure 28
The IF and IA of the sample signal fsig6: (a) IF and (b) IA.
Figure 29
Figure 29
The waveforms of EWT result of fsig6 and the corresponding Fourier spectrums: (a) waveforms and (b) Fourier spectrums.
Figure 30
Figure 30
The waveform of the sample signal fsig7.
Figure 31
Figure 31
The STFT of the sample signal fsig7: (a) 2D figure and (b) 3D figure.
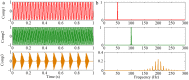
Figure 32
Figure 32
Each component of the sample signal fsig7: (a) the waveform and (b) the Fourier spectrum.
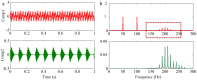
Figure 33
Figure 33
The waveforms of EWT result of fsig6 and the corresponding Fourier spectrums: (a) waveforms and (b) Fourier spectrums. The parameters used in processed code are as follows: params.detect is set as ‘adaptivereg’, params.typeDetect is set as ‘otsu’.
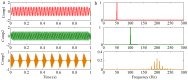
Figure 34
Figure 34
The decomposition result of fsig7: (a) the waveform and (b) the Fourier spectrum.
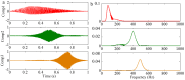
Figure 35
Figure 35
The decomposition result of fsig6 by using VMD: (a) the waveform and (b) the Fourier spectrum.
Figure 36
Figure 36
The STFT representations of the Comps 1–3: (a) Comp 1; (b) Comp 2 and (c) Comp 3.
Figure 37
Figure 37
The decomposition result of fsig6 by using EMD: (a) the waveform and (b) the Fourier spectrum.
Figure 38
Figure 38
The STFT representations of the IMFs 1–3: (a) IMF 1; (b) IMF 2; and (c) IMF 3.
Figure 39
Figure 39
The waveform of the sample signal fsig8.
Figure 40
Figure 40
The STFT of the sample signal fsig8: (a) 2D figure and (b) 3D figure.
Figure 41
Figure 41
The waveforms of decomposition result of fsig8 by using VKF_OT and the corresponding calculation errors: (a) waveforms and (b) calculation errors.
Figure 42
Figure 42
The waveform of the sample signal fsig9.
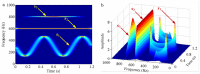
Figure 43
Figure 43
The STFT of the sample signal fsig9: (a) 2D figure and (b) 3D figure.
Figure 44
Figure 44
The IF errors of the sample signal fsig9 obtained from the corresponding STFTs.
Figure 45
Figure 45
The waveforms of decomposition result of fsig9 by using VKF_OT and the corresponding calculation errors: (a) waveforms and (b) calculation errors.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Huang N.E., Shen Z., Long S.R., Wu M.C., Shih H.H., Zheng Q., Yen N.C., Tung C.C., Liu H.H. The empirical mode decomposition and the Hilbert spectrum for non-linear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998;454:903–995. doi: 10.1098/rspa.1998.0193. - DOI
    1. Feng Z., Zhang D., Zuo M.J. Adaptive Mode Decomposition Methods and Their Applications in Signal Analysis for Machinery Fault Diagnosis: A Review with Examples. IEEE Access. 2017;5:24301–24331. doi: 10.1109/ACCESS.2017.2766232. - DOI
    1. Peng Z.K., Chu F.L. Application of the wavelet transform in machine condition monitoring and fault diagnostics: A review with bibliography. Mech. Syst. Signal Process. 2004;18:199–221. doi: 10.1016/S0888-3270(03)00075-X. - DOI
    1. Nguyen H.N., Kim J., Kim J.M. Optimal Sub-Band Analysis Based on the Envelope Power Spectrum for Effective Fault Detection in Bearing under Variable, Low Speeds. Sensors. 2018;18:1389. doi: 10.3390/s18051389. - DOI - PMC - PubMed
    1. Baek W., Baek S., Kim D.Y. Characterization of System Status Signals for Multivariate Time Series Discretization Based on Frequency and Amplitude Variation. Sensors. 2018;18:154. doi: 10.3390/s18010154. - DOI - PMC - PubMed

LinkOut - more resources