Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2018 May 1:544:350-369.
doi: 10.1016/j.laa.2018.01.019. Epub 2018 Mar 6.

Gram Determinants of Real Binary Tensors

Anna Seigal

Gram Determinants of Real Binary Tensors

Anna Seigal. Linear Algebra Appl. .

Abstract

A binary tensor consists of 2 n entries arranged into hypercube format 2 × 2 × ⋯ × 2. There are n ways to flatten such a tensor into a matrix of size 2 × 2 n-1. For each flattening, M, we take the determinant of its Gram matrix, det(MMT ). We consider the map that sends a tensor to its n-tuple of Gram determinants. We propose a semi-algebraic characterization of the image of this map. This offers an answer to a question raised by Hackbusch and Uschmajew concerning the higher-order singular values of tensors.

Keywords: Tensors; semi-algebraic geometry; singular value decomposition; sum-of-squares.

PubMed Disclaimer

Figures

Figure 1
Figure 1
The minors unique to flattenings one, two and three respectively
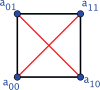
Figure 2
Figure 2
The minors unique to one flattening are represented by edges. The black edges are minors from flattenings two or three. The red diagonal edges are from flattening one.
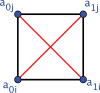
Figure 3
Figure 3
A copy of D3(3) inside Dm(m)
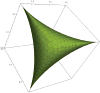
Figure 4
Figure 4
The surface Q = 0
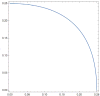
Figure 5
Figure 5
The surface Q = 0 meets the plane d1 = 1/4
Figure 6
Figure 6
The surface Q = 0 in singular value coordinates. The black dot is Example 3.1.
See this image and copyright information in PMC

References

    1. Choi MD, Lam TY, Reznick B. Sums of Squares of Real Polynomials. Proceedings of Symposia in Pure Mathematics. 1995;58(2):103–126.
    1. Domokos M. Discriminant of Symmetric Matrices as a Sum of Squares and the Orthogonal Group. Communications on Pure and Applied Mathematics. 2011;64(4):443–465.
    1. Grayson D, Stillman M. Macaulay2, a Software System for Research in Algebraic Geometry. available at www.math.uiuc.edu/Macaulay2/
    1. Landsberg JM. Graduate Studies in Mathematics. Vol. 128. American Mathematical Society; Providence RI: 2012. Tensors: Geometry and Applications.
    1. De Lathauwer L, De Moor B, Vandewalle J. A Multilinear Singular Value Decomposition. SIAM J. Matrix Anal. Appl. 2000;21(4):1253–1278.

LinkOut - more resources