Beating the channel capacity limit for superdense coding with entangled ququarts
- PMID: 30035231
- PMCID: PMC6054506
- DOI: 10.1126/sciadv.aat9304
Beating the channel capacity limit for superdense coding with entangled ququarts
Abstract
Quantum superdense coding protocols enhance channel capacity by using shared quantum entanglement between two users. The channel capacity can be as high as 2 when one uses entangled qubits. However, this limit can be surpassed by using high-dimensional entanglement. We report an experiment that exceeds the limit using high-quality entangled ququarts with fidelities up to 0.98, demonstrating a channel capacity of 2.09 ± 0.01. The measured channel capacity is also higher than that obtained when transmitting only one ququart. We use the setup to transmit a five-color image with a fidelity of 0.952. Our experiment shows the great advantage of high-dimensional entanglement and will stimulate research on high-dimensional quantum information processes.
Figures
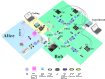
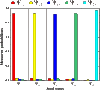


References
-
- Horodecki R., Horodecki P., Horodecki M., Horodecki K., Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009).
-
- Bennett C. H., Wiesner S. J., Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states. Phys. Rev. Lett. 69, 2881–2884 (1992). - PubMed
-
- Mattle K., Weinfurter H., Kwiat P. G., Zeilinger A., Dense coding in experimental quantum communication. Phys. Rev. Lett. 76, 4656–4659 (1996). - PubMed
-
- Li X., Pan Q., Jing J., Zhang J., Xie C., Peng K., Quantum dense coding exploiting a bright Einstein-Podolsky-Rosen beam. Phys. Rev. Lett. 88, 047904 (2002). - PubMed
-
- Fang X., Zhu X., Feng M., Mao X., Du F., Experimental implementation of dense coding using nuclear magnetic resonance. Phys. Rev. A 61, 022307 (2000).
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

