Waves in strongly nonlinear discrete systems

Abstract

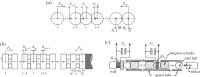
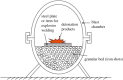
The paper presents the main steps in the development of the strongly nonlinear wave dynamics of discrete systems. The initial motivation was prompted by the challenges in the design of barriers to mitigate high-amplitude compression pulses caused by impact or explosion. But this area poses a fundamental mathematical and physical problem and should be considered as a natural step in developing strongly nonlinear wave dynamics. Strong nonlinearity results in a highly tunable behaviour and allows design of systems with properties ranging from a weakly nonlinear regime, similar to the classical case of the Fermi-Pasta-Ulam lattice, or to a non-classical case of sonic vacuum. Strongly nonlinear systems support periodic waves and one of the fascinating results was a discovery of a strongly nonlinear solitary wave in sonic vacuum (a limiting case of a periodic wave) with properties very different from the Korteweg de Vries solitary wave. Shock-like oscillating and monotonous stationary stress waves can also be supported if the system is dissipative. The paper discusses the main theoretical and experimental results, focusing on travelling waves and possible future developments in the area of strongly nonlinear metamaterials.This article is part of the theme issue 'Nonlinear energy transfer in dynamical and acoustical systems'.

Keywords: discrete systems; shock waves; solitons; sonic vacuum; strongly nonlinear.

Figure 1.

Contact deformation in pulse propagating in weakly precompressed chains of spherical beads (a), and in a chain of cylinders with O-rings responsible for strongly nonlinear double power-law interaction between cylinders (b) and non-compressed chain of spheres and tungsten cylinders with embedded gauges inside cylinders impacted by a striker (c).

Figure 2.

Train of Nesterenko solitary waves reflected from a steel wall. The time scale is 50 µs per large horizontal division, vertical scale 18.3 N between large divisions.

Figure 3.

Oscillatory ‘shock’ wave in the chain of steel spheres (a) and monotonous ‘shock’ (b) in the chain of lead spheres reflected from a steel wall. Number of spheres in both chains 20, striker mass 30 m, where m is the mass of steel sphere, velocity 1 m s⁻¹. Diameter of spheres in both cases was 4.75 mm. Time scale: (a) 50 µs, (b) 200 µs per large horizontal division, vertical scale 92N (a) and 18.5N (b) between large vertical divisions. (Online version in colour.)

Figure 4.

Blast chamber with a granular bed made from iron shots as a supporting barrier.

Figure 5.

Indentations on the lead plate at the bottom of the granular bed made from iron shots at different distances from contact explosion: 50 mm (a) and 100 mm (b). (Online version in colour.)