A mean field view of the landscape of two-layer neural networks
- PMID: 30054315
- PMCID: PMC6099898
- DOI: 10.1073/pnas.1806579115
A mean field view of the landscape of two-layer neural networks
Abstract
Multilayer neural networks are among the most powerful models in machine learning, yet the fundamental reasons for this success defy mathematical understanding. Learning a neural network requires optimizing a nonconvex high-dimensional objective (risk function), a problem that is usually attacked using stochastic gradient descent (SGD). Does SGD converge to a global optimum of the risk or only to a local optimum? In the former case, does this happen because local minima are absent or because SGD somehow avoids them? In the latter, why do local minima reached by SGD have good generalization properties? In this paper, we consider a simple case, namely two-layer neural networks, and prove that-in a suitable scaling limit-SGD dynamics is captured by a certain nonlinear partial differential equation (PDE) that we call distributional dynamics (DD). We then consider several specific examples and show how DD can be used to prove convergence of SGD to networks with nearly ideal generalization error. This description allows for "averaging out" some of the complexities of the landscape of neural networks and can be used to prove a general convergence result for noisy SGD.
Keywords: Wasserstein space; gradient flow; neural networks; partial differential equations; stochastic gradient descent.
Copyright © 2018 the Author(s). Published by PNAS.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
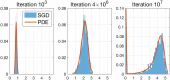
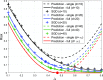
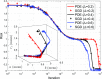
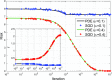
References
-
- Rosenblatt F. Principles of Neurodynamics. Spartan Book; Washington, DC: 1962.
-
- Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. In: Vardi MY, editor. Advances in Neural Information Processing Systems. Association for Computing Machinery; New York: 2012. pp. 1097–1105.
-
- Goodfellow I, Bengio Y, Courville A, Bengio Y. Deep Learning. Vol 1 MIT Press; Cambridge: 2016.
-
- Robbins H, Monro S. A stochastic approximation method. Ann Math Stat. 1951;22:400–407.
-
- Bottou L. Large-scale machine learning with stochastic gradient descent. In: Lechevallier Y, Saporta G, editors. Proceedings of COMPSTAT’2010. Physica; Heidelberg: 2010. pp. 177–186.
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases
Miscellaneous

