Inter-trial effects in visual pop-out search: Factorial comparison of Bayesian updating models
- PMID: 30059500
- PMCID: PMC6091979
- DOI: 10.1371/journal.pcbi.1006328
Inter-trial effects in visual pop-out search: Factorial comparison of Bayesian updating models
Abstract
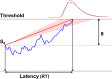
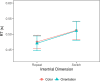
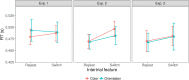
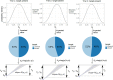
Many previous studies on visual search have reported inter-trial effects, that is, observers respond faster when some target property, such as a defining feature or dimension, or the response associated with the target repeats versus changes across consecutive trial episodes. However, what processes drive these inter-trial effects is still controversial. Here, we investigated this question using a combination of Bayesian modeling of belief updating and evidence accumulation modeling in perceptual decision-making. In three visual singleton ('pop-out') search experiments, we explored how the probability of the response-critical states of the search display (e.g., target presence/absence) and the repetition/switch of the target-defining dimension (color/ orientation) affect reaction time distributions. The results replicated the mean reaction time (RT) inter-trial and dimension repetition/switch effects that have been reported in previous studies. Going beyond this, to uncover the underlying mechanisms, we used the Drift-Diffusion Model (DDM) and the Linear Approach to Threshold with Ergodic Rate (LATER) model to explain the RT distributions in terms of decision bias (starting point) and information processing speed (evidence accumulation rate). We further investigated how these different aspects of the decision-making process are affected by different properties of stimulus history, giving rise to dissociable inter-trial effects. We approached this question by (i) combining each perceptual decision making model (DDM or LATER) with different updating models, each specifying a plausible rule for updating of either the starting point or the rate, based on stimulus history, and (ii) comparing every possible combination of trial-wise updating mechanism and perceptual decision model in a factorial model comparison. Consistently across experiments, we found that the (recent) history of the response-critical property influences the initial decision bias, while repetition/switch of the target-defining dimension affects the accumulation rate, likely reflecting an implicit 'top-down' modulation process. This provides strong evidence of a disassociation between response- and dimension-based inter-trial effects.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures



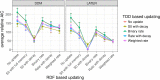
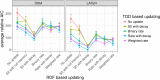
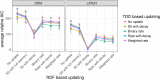
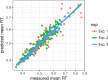

References
-
- Maljkovic V, Nakayama K. Priming of pop-out: II. The role of position. Percept Psychophys. 1996;58: 977–991. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

