Successful structure learning from observational data
- PMID: 30064655
- PMCID: PMC6086386
- DOI: 10.1016/j.cognition.2018.06.003
Successful structure learning from observational data
Abstract
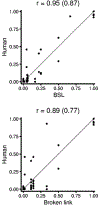
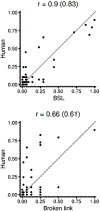
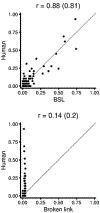
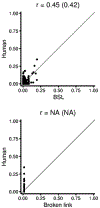
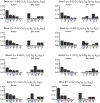
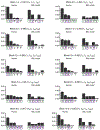
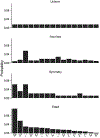
Previous work suggests that humans find it difficult to learn the structure of causal systems given observational data alone. We identify two conditions that enable successful structure learning from observational data: people succeed if the underlying causal system is deterministic, and if each pattern of observations has a single root cause. In four experiments, we show that either condition alone is sufficient to enable high levels of performance, but that performance is poor if neither condition applies. A fifth experiment suggests that neither determinism nor root sparsity takes priority over the other. Our data are broadly consistent with a Bayesian model that embodies a preference for structures that make the observed data not only possible but probable.
Keywords: Bayesian modeling; Causal reasoning; Causal structure learning.
Copyright © 2018 Elsevier B.V. All rights reserved.
Figures



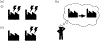
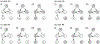










References
-
- Boddez Y, Houwer JD, & Beckers T (2017). The inferential reasoning theory of causal learning: Towards a multi-process propositional account In The Oxford Handbook of Causal Reasoning (p. 53). Oxford University Press.
-
- Bonawitz EB, & Lombrozo T (2012). Occam’s rattle: Children’s use of simplicity and probability to constrain inference. Developmental Psychology, 48, 1156–1164. - PubMed
-
- Bramley NR, Dayan P, Griffiths TL, & Lagnado DA (2017). Formalizing Neurath’s ship: Approximate algorithms for online causal learning. Psychological Review,. - PubMed
-
- Cheng PW (1997). From covariation to causation: a causal power theory. Psychological Review, 104, 367–405.
-
- Chi MTH, Roscoe RD, Slotta JD, Roy M, & Chase CC (2012). Misconceived causal explanations for emergent processes. Cognitive Science, 36, 1–61. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

