A mechanism for bistability in glycosylation

Abstract

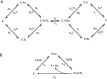
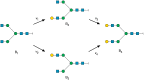
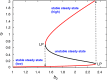
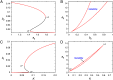
Glycosyltransferases are a class of enzymes that catalyse the posttranslational modification of proteins to produce a large number of glycoconjugate acceptors from a limited number of nucleotide-sugar donors. The products of one glycosyltransferase can be the substrates of several other enzymes, causing a combinatorial explosion in the number of possible glycan products. The kinetic behaviour of systems where multiple acceptor substrates compete for a single enzyme is presented, and the case in which high concentrations of an acceptor substrate are inhibitory as a result of abortive complex formation, is shown to result in non-Michaelian kinetics that can lead to bistability in an open system. A kinetic mechanism is proposed that is consistent with the available experimental evidence and provides a possible explanation for conflicting observations on the β-1,4-galactosyltransferases. Abrupt switching between steady states in networks of glycosyltransferase-catalysed reactions may account for the observed changes in glycosyl-epitopes in cancer cells.

Fig 1. Enzyme mechanisms.

A. Random-order addition of substrates, under reversible, rapid-equilibrium conditions. B. Compulsory-order addition of substrates, with quasi-steady-state assumptions.

Fig 2. Model scheme of GalT acting on a diantennary N-glycan, in which species B₁, B₂ and B₃ are competing substrates.

Sugar symbols used, in SNFG notation [32]: blue square, GlcNAc; green circle, Man; yellow circle, Gal.

Fig 3. Substrate inhibition by one or more substrates.

A. Reaction scheme for the formation of ternary enzyme-acceptor complex; the binding of Ax to the E⋅B_j complex (shown in grey) only occurs within the random order model. B. Substrate inhibition of an enzyme with a single acceptor, for three different donor concentrations (0.5, 5, 50) with $K_{\text{m}}^{\text{Ax}}=0.5$. C. Total enzyme initial rate as a function of two substrates, B₁ and B₂, exhibiting substrate inhibition through formation of an abortive (dead-end) ternary complex. D. Bistability exhibited by a substrate-inhibited enzyme (Eq (7)) in a system open to substrate, for three different values of the concentration of acceptor available externally: [B]₀ = 0.666 (red), [B]₀ = 2.000 (orange), [B]₀ = 3.333 (green). At [B]₀ = 2.0, the line intercepts the velocity–substrate curve at three points, the two outer points being stable, and the inner an unstable steady-state solution.

Fig 4. Bistability in an open system for a bisubstrate enzyme reaction exhibiting inhibition at high substrate concentrations.

Shown is a bifurcation diagram of the one-dimensional ODE system given by Eq (11), with the external concentration of acceptor substrate, b₀, as the bifurcation parameter. The donor is assumed to be buffered to a constant concentration. The stable steady state levels of the acceptor, b, are indicated by the red curves, the black curve denoting the unstable steady state. An exchange of stability between the stable and unstable branches occurs at the limit points (LP), b₀ = 1.518665 and b₀ = 2.325853, as indicated by the dashed lines. Other parameters of the model are given in the text.

Fig 5. Bistability in an open reaction system described by the ODE system of Eqs (12)–(16), based on the reactions of Fig 2.

Parameters of the model are given in Table 1. A. Steady-state levels of b₂ as the external concentration of donor substrate, a₀, is varied, with b₀ = 0.3; limit points (LP) separate the branches of stable (red curve) and unstable (black curve) steady states. B. Cusp in a₀–b₀ space, with branches of limit points enclosing a region of bistability. C. Steady-state levels of initial substrate, b₁, as the diffusion constant, K, is varied. D. Region of bistability in a₀–K space, with terminal limit points as indicated.