Solving high-dimensional partial differential equations using deep learning
- PMID: 30082389
- PMCID: PMC6112690
- DOI: 10.1073/pnas.1718942115
Solving high-dimensional partial differential equations using deep learning
Abstract
Developing algorithms for solving high-dimensional partial differential equations (PDEs) has been an exceedingly difficult task for a long time, due to the notoriously difficult problem known as the "curse of dimensionality." This paper introduces a deep learning-based approach that can handle general high-dimensional parabolic PDEs. To this end, the PDEs are reformulated using backward stochastic differential equations and the gradient of the unknown solution is approximated by neural networks, very much in the spirit of deep reinforcement learning with the gradient acting as the policy function. Numerical results on examples including the nonlinear Black-Scholes equation, the Hamilton-Jacobi-Bellman equation, and the Allen-Cahn equation suggest that the proposed algorithm is quite effective in high dimensions, in terms of both accuracy and cost. This opens up possibilities in economics, finance, operational research, and physics, by considering all participating agents, assets, resources, or particles together at the same time, instead of making ad hoc assumptions on their interrelationships.
Keywords: Feynman–Kac; backward stochastic differential equations; deep learning; high dimension; partial differential equations.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

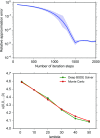

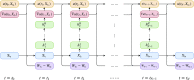
References
-
- Bellman RE. Dynamic Programming. Princeton Univ Press; Princeton: 1957.
-
- Goodfellow I, Bengio Y, Courville A. Deep Learning. MIT Press; Cambridge, MA: 2016.
-
- LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015;521:436–444. - PubMed
-
- Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. In: Bartlett P, Pereira F, Burges CJC, Bottou L, Weinberger KQ, editors. Advances in Neural Information Processing Systems. Vol 25. Curran Associates, Inc.; Red Hook, NY: 2012. pp. 1097–1105.
-
- Hinton G, et al. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Process Mag. 2012;29:82–97.
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

